Definition:
f is a linear map if
-
f of v + w = f of v + f of w for all v, w
-
f of lambda v = lambda times f of v for all v and all lambda in R.
39. Kernels
39. Kernels
Definition of the kernel
Recall the following definitions:
Definition:
V is a linear subspace if
-
v and w are in V implies v + w is in V
-
v in V implies lambda v is in V for all lambda in R.
These two definitions are very similar. We will exploit this in the next two videos: given a linear map f from R^n to R^m, we will associate to it two subspaces ker of f inside R^n (the kernel of f) and im of f (the image of f).
Definition:
The kernel of f is the set of v in R^n such that f of v = 0. (If m = n then this is just the 0-eigenspace of f).
Example:
Let f fromR^3 to R^3 be the map f of v equals A v for A = 1, 0, 0; 0, 1, 0; 0, 0, 0. Note that f of x, y, z = x, y, 0. This is the vertical projection to the x y-plane.
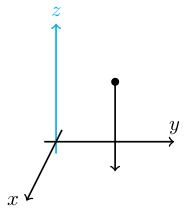
The kernel of f is the z-axis (blue in the figure; these are the points which project vertically down to the origin). That is ker f equals the set of vectors of the form 0, 0, z.
Example:
Recall the example of a 2-by-3 matrix A = 1, 0, minus 1; 0, 1, minus 1 (going from R^3 to R^2) from Video 3. This projects vectors into the plane; if we think of R^2 as the x y-plane then we can visualise this map as the projection of vectors in the minus 1, minus 1, minus 1-direction until they live in the x y-plane.
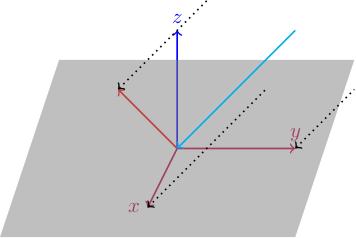
We described this as projecting light rays in the minus 1, minus 1, minus 1 direction. In this case, the kernel of A is precisely the light ray which hits the origin, which is the line of vectors of the form x, x, x (light blue in the picture).
Kernel is a subspace
Lemma:
The kernel is a subspace.
Given v and w in ker f, we need to show that v + w is in ker f. Since v, w in ker f, we know that f of v = f of w = 0. Therefore f of v + w = f of v + f of w (since f is linear) which equals 0 + 0, which equals 0, so v + w is in ker f. Similarly, f of lambda v equals lambda times f of v, which equals lambda times 0, which equals 0.
Remarks
-
0 in ker f for any linear map f because f of 0 = 0.
-
If f is invertible then ker of f = 0: if v is in ker f then v = f inverse 0, which equals 0.
-
The "kernel" in a nut is the little bit in the middle that's left when you strip away the husk. If f of v = A v then we can think of ker f as the space of solutions to the simultaneous equations A v = 0, which is the intersection of the hyperplanes A_{1, 1}v_1 + dot dot dot + A_{1 n} v_n = 0, A_{2, 1}v_1 + dot dot dot + A_{2 n} v_n = 0, up to A_{m, 1}v_1 + dot dot dot + A_{m n} v_n = 0. In other words, it's the little bit left over when you've intersected all these hyperplanes.
Simultaneous equations revisited
Lemma:
Consider the simultaneous equations A v = b (A is an m-by-n matrix and b is in R^m). Let f of v = A v. The space of solutions to A v = b, if nonempty, is an affine translate of ker f.
Example:
If A = 1, 0, 0; 0, 1, 0; 0, 0, 0 (so f is vertical projection to the x y-plane) then A v = b has a solution only if b is in the x y-plane, and in that case it has a whole vertical line of solutions sitting above b.
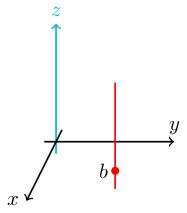
This vertical line of solutions is parallel to the kernel of f (the z-axis), i.e. it is a translate of the kernel.
We saw this lemma earlier in a different guise in Video 19. Namely, we saw that if v_0 is a solution to A v = b then the set of all solutions is the affine subspace v_0 + U where U is the space of solutions to A v = 0. In other words, U = ker f.
In particular, we see that if A v = b has a solution then it has a k-dimensional space of solutions, where k is the dimension of ker f.
Remember that the space of solutions has dimension equal to the number of free variables when we put A into reduced echelon form. For example, A = 1, 0, 0; 0, 1, 0; 0, 0, 0 is in reduced echelon form with two leading entries and one free variable, which is why we get 1-dimensional solution spaces.
Definition:
The nullity of A (or of f) is the dimension of ker f (i.e. the number of free variables of A when put into reduced echelon form).
Our goal for the next video is to prove the rank-nullity theorem which gives us a nice formula relating the nullity to another important number called the rank.