Weight space decomposition

Weight spaces

0.00 We now embark on our study of the fine structure of $SU(2)$ representations, aiming towards the classification theorem for irreducible representations that we stated earlier.

The first key observation is that $SU(2)$ contains a subgroup $T$ isomorphic to $U(1)$ : $T=\left\{\begin{pmatrix}e^{i\theta}&0\\ 0&e^{-i\theta}\end{pmatrix}\ :\ e^{i\theta}\in U(1)\right\}.$

0.55 If I have a complex representation $R\colon SU(2)\to GL(V)$ then I can restrict it to $T$ and I get a representation $R|_{T}\colon T\to GL(V)$ . By the classification of irreps of $U(1)$ , we find that $V=V_{1}\oplus\cdots\oplus V_{n}$ where $n=\dim V$ and, with respect to this splitting, $R\begin{pmatrix}e^{i\theta}&0\\ 0&e^{-i\theta}\end{pmatrix}$ is the diagonal matrix $\begin{pmatrix}e^{im_{1}\theta}&&{\large 0}\\ &\ddots&\\ {\large 0}&&e^{im_{n}\theta}\end{pmatrix}$ . The $m_{1},\ldots,m_{n}$ are integers called the weights, the $V_{i}$ are called weight spaces, and the direct sum is called the weight space decomposition.

Remark:

2.30 It's important to note that this is not a decomposition of $V$ as a representation of $SU(2)$ , only as a representation of $T$ . In particular, if you act with a non-diagonal matrix in $SU(2)$ then it will mix up these subspaces $V_{i}$ .

Example

Example:

3.50 Take the standard representation $R\colon SU(2)\to GL(2,\mathbf{C})$ . We have $R\begin{pmatrix}e^{i\theta}&0\\ 0&e^{-i\theta}\end{pmatrix}=\begin{pmatrix}e^{i\theta}&0\\ 0&e^{-i\theta}\end{pmatrix}$ . This is already diagonal. The weight spaces are spanned by the vectors $(1,0)$ and $(0,1)$ and the weights are $1$ and $-1$ respectively.

5.00 We will depict the weight space decomposition as follows (the weight diagram). Consider the integer points sitting on the number line. Colour in each integer $m$ which appears as a weight, and label it by the number of $V_{i}$ having weight $m$ if this number is strictly bigger than 1. In the example above, the weight diagram is a blob at $-1$ and a blob at $1$ .

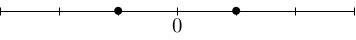
The weight space decomposition of the standard rep of SU(2), consisting of a blob at minus 1 and a blob at 1

Example:

5.50 Consider the representation $R\colon SU(2)\to GL(\mathfrak{su}(2)\otimes\mathbf{C})$ , $R(g)M_{v}=gM_{v}g^{-1}$ . We computed the associated Lie algebra homomorphism $R_{*}\colon\mathfrak{su}(2)\to\mathfrak{gl}(3,\mathbf{C})$ . We found that $R_{*}\begin{pmatrix}ix&y+iz\\ -y+iz&-ix\end{pmatrix}=\begin{pmatrix}0&-2z&2y\\ 2z&0&-2x\\ -2y&2x&0\end{pmatrix}.$ Since we're interested in the diagonal subgroup $T$ we can set $y=z=0$ . We're interested in $R\left(\exp\begin{pmatrix}ix&0\\ 0&-ix\end{pmatrix}\right)=\exp\left(R_{*}\begin{pmatrix}ix&0\\ 0&-ix\end{pmatrix}\right)$ 7.15 which gives $\exp\begin{pmatrix}0&0&0\\ 0&0&-2x\\ 0&2x&0\end{pmatrix}=\begin{pmatrix}1&0&0\\ 0&\cos 2x&-\sin 2x\\ 0&\sin 2x&\cos 2x\end{pmatrix}.$ 8.00 The weights are going to be $-2,0,2$ . This is because:

We calculated the weights of the representation $U(1)\to GL(2,\mathbf{C})$ , $e^{i\theta}\mapsto\begin{pmatrix}\cos\theta&-\sin\theta\\ \sin\theta&\cos\theta\end{pmatrix}$ : these were $\pm 1$ because with respect to a basis of eigenvectors this matrix diagonalised and became $\begin{pmatrix}e^{i\theta}&0\\ 0&e^{-i\theta}\end{pmatrix}$ .
8.30 We're looking at the same submatrix but with $2\theta$ everywhere instead of $\theta$ , so this submatrix can be diagonalised to give $\begin{pmatrix}e^{i2\theta}&0\\ 0&e^{-i2\theta}\end{pmatrix}$ .
What's left is the top-left entry which is $1=e^{i0\theta}$ , so we also get a weight space with weight 0.

9.25 The weight diagram is therefore:

The weight diagram of the 3-dimensional irrep of SU(2): blobs sitting at -2, 0, 2

Example:

9.50 Take $\mathrm{Sym}^{2}(\mathbf{C}^{2})$ . If $e_{1}$ and $e_{2}$ form the standard basis for the standard representation then this has basis $e_{1}^{2}$ , $e_{1}e_{2}$ , $e_{2}^{2}$ . Since $\begin{pmatrix}e^{i\theta}&0\\ 0&e^{-i\theta}\end{pmatrix}$ acts as $e_{1}\mapsto e^{i\theta}e_{1}\mbox{ and }e_{2}\mapsto e^{-i\theta}e_{2}$ in the standard representation, $\mathrm{Sym}^{2}\begin{pmatrix}e^{i\theta}&0\\ 0&e^{-i\theta}\end{pmatrix}$ acts as $e_{1}^{2}\mapsto e^{i2\theta}e_{1}^{2},\ e_{1}e_{2}\mapsto e_{1}e_{2},\ e_{2}^% {2}\mapsto e^{-i2\theta}e_{2}^{2}$ (each factor transforms under the standard representation and then you multiply them together and the factors of $e^{i\theta}$ or $e^{-i\theta}$ either combine or cancel).

11.50 The weight spaces are therefore:

$V_{1}=\mathbf{C}\cdot e_{1}^{2}$ , with weight $2$ ,
$V_{2}=\mathbf{C}\cdot e_{1}e_{2}$ , with weight $0$ ,
$V_{3}=\mathbf{C}\cdot e_{2}^{2}$ , with weight $-2$ .

The weight diagram is therefore the same as the weight diagram for the previous example:

The weight diagram of Sym 2 of the standard representation of SU(2): blobs sitting at -2, 0, 2. This is the same as the weight diagram from the earlier example.

12.30 We'll see later that this is enough to tell us that these representations are isomorphic.

Pre-class exercise

Exercise:

Figure out the weight diagram for $\mathrm{Sym}^{n}(\mathbf{C}^{2})$ .