X and Y

From su(2) to sl(2,C)

0.00 Last time we saw that, given a complex representation $R\colon SU(2)\to GL(V)$ there is a weight space decomposition $V=\bigoplus_{j=1}^{n}V_{j}$ such that with respect to this splitting, $R\begin{pmatrix}e^{i\theta}&0\\ 0&e^{-i\theta}\end{pmatrix}$ is the diagonal matrix

$\begin{pmatrix}e^{im_{1}\theta}&&{\large 0}\\ &\ddots&\\ {\large 0}&&e^{im_{n}\theta}\end{pmatrix}$ where

$m_{j}\in\mathbf{Z}$ are the weights of the representation.

1.00 At the level of Lie algebras, we have

$R\left(\exp\theta\begin{pmatrix}i&0\\ 0&-i\end{pmatrix}\right)=\exp\theta R_{*}\begin{pmatrix}i&0\\ 0&-i\end{pmatrix},$ so

$R_{*}\begin{pmatrix}i&0\\ 0&-i\end{pmatrix}=\begin{pmatrix}im_{1}\theta&&{\large 0}\\ &\ddots&\\ {\large 0}&&im_{n}\end{pmatrix}.$

2.05 In other words, we know where one of the matrices in $\mathfrak{su}(2)$ goes under $R_{*}$ . But there are other matrices in $\mathfrak{su}(2)$ : the general element is $\begin{pmatrix}ix&y+iz\\ -y+iz&-ix\end{pmatrix}$ ; where do these go?

2.55 Pick the basis

$\sigma_{1}=\begin{pmatrix}i&0\\ 0&-i\end{pmatrix},\ \sigma_{2}=\begin{pmatrix}0&1\\ -1&0\end{pmatrix},\ \sigma_{3}=\begin{pmatrix}0&i\\ i&0\end{pmatrix}$ for

$\mathfrak{su}(2)$ (corresponding to the

$x$ ,

$y$ and

$z$ directions). These (or closely related versions of them) are often called the Pauli matrices.

3.40 I've told you what $R_{*}\sigma_{1}$ is, and since $R_{*}$ is linear (determined by its values on a basis) it's enough to say what $R_{*}\sigma_{2}$ and $R_{*}\sigma_{3}$ are to determine $R_{*}$ completely. It turns out to be much easier to use:

$X=\frac{1}{2}(\sigma_{2}-i\sigma_{3})=\begin{pmatrix}0&1\\ 0&0\end{pmatrix},\qquad Y=-\frac{1}{2}(\sigma_{2}+i\sigma_{3})=\begin{pmatrix}% 0&0\\ 1&0\end{pmatrix}.$

4.45 The problem is that these correspond to complex values of $y$ and $z$ , so they don't live in $\mathfrak{su}(2)$ . Instead, they live in $\mathfrak{su}(2)\otimes\mathbf{C}$ . In fact, $X$ and $Y$ live in $\mathfrak{sl}(2,\mathbf{C})$ and $\sigma_{1}$ is equal to $i H$ where $H=\begin{pmatrix}1&0\\ 0&-1\end{pmatrix}$ . So it turns out that $\mathfrak{su}(2)\otimes\mathbf{C}=\mathfrak{sl}(2,\mathbf{C})$ : anything inside $\mathfrak{sl}(2,\mathbf{C})$ can be written as a complex linear combination of $\sigma_{1},\sigma_{2},\sigma_{3}$ and anything inside $\mathfrak{su}(2)\otimes\mathbf{C}$ can be written as a complex linear combination of $X$ , $Y$ , and $H$ .

6.15 If $R_{*}\colon\mathfrak{su}(2)\to\mathfrak{gl}(V)$ is a representation of Lie algebras where $V$ is a complex vector space, then we get for free a representation $R_{*}^{\mathbf{C}}\colon\mathfrak{su}(2)\otimes\mathbf{C}\to\mathfrak{gl}(V)$ , just by setting $R_{*}^{\mathbf{C}}(M_{1}+iM_{2})=R_{*}M_{1}+iR_{*}M_{2}$ .

Remark:

6.55 The point is that we don't know what $i M$ means if $M\in\mathfrak{su}(2)$ because $\mathfrak{su}(2)$ is a real Lie algebra so we need to complexify it, but we do know what $iR_{*}M\in\mathfrak{gl}(V)$ means because $\mathfrak{gl}(V)$ is a complex Lie algebra and we don't to complexify it.

How do X and Y act?

Definition:

7.40 Let $R\colon SU(2)\to GL(V)$ be a complex representation and write $W_{m}=\bigoplus_{m_{j}=m}V_{j}$ for the sum of all subspaces with weight $m$ . In other words, we're grouping the irreducible subrepresentations for the diagonal $U(1)$ into subspaces with a common weight. We'll call $W_{m}$ the weight space with weight $m$ .

Example:

For $\mathrm{Sym}^{2}(\mathbf{C}^{2})$ , $W_{-2}$ , $W_{0}$ and $W_{2}$ are each 1-dimensional (spanned by $e_{2}^{2}$ , $e_{1}e_{2}$ and $e_{1}^{2}$ respectively). We draw this as a weight diagram:

The weight diagram of Sym 2 of the standard representation of SU(2), with blobs at -2, 0 and 2

Lemma:

9.00 The following lemma tells us how $H$ , $X$ and $Y$ act in the representation:

$R_{*}^{\mathbf{C}}(H)$ acts on $W_{m}$ as $m I$ , i.e. if $v\in W_{m}$ then $R_{*}^{\mathbf{C}}(H)v=mv$ .
9.30 $R_{*}^{\mathbf{C}}(X)$ sends $W_{m}$ to $W_{m+2}$ , i.e. if $v\in W_{m}$ then $R_{*}^{\mathbf{C}}(X)v\in W_{m+2}$ .
$R_{*}^{\mathbf{C}}(Y)$ sends $W_{m}$ to $W_{m-2}$ .

Remark:

In terms of the weight diagram earlier, we can draw arrows which show how $H$ , $X$ and $Y$ act: $H$ sends the weight spaces back to themselves, $X$ shifts to the right, and $Y$ shifts to the left. Note that in the example of $\mathrm{Sym}^{2}(\mathbf{C}^{2})$ , $X$ sends $W_{2}$ to $W_{4}$ , but $W_{4}=0$ , so $X$ annihilates elements of $W_{2}$ .

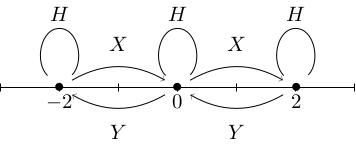
Arrows on the weight diagram indicating how X, Y and H act

Remark:

11.00 This is what I meant when I said that the off-diagonal elements of $\mathfrak{su}(2)$ mix up the weight spaces: they do so in a very precise way. Also, you can see why $X$ and $Y$ are more convenient than $\sigma_{2}$ and $\sigma_{3}$ : these would mix up weight spaces in a messy way that combines the $X$ and $Y$ arrows.

Proof:

11.30 We have already proved part (1) of the lemma: we know that $v\in W_{m}$ implies $R_{*}(\sigma_{1})v=imv$ , and $\sigma_{1}=iH$ , so $R_{*}^{\mathbf{C}}(H)v=mv$ .
12.30 We'll do (2) and leave the very-similar (3) as an exercise. I'll drop the superscript $\mathbf{C}$ from now on. Suppose that $v\in W_{m}$ . We want to show that $R_{*}(X)v\in W_{m+2}$ . Note that $v\in W_{m}$ if and only if $R_{*}(H)v=mv$ and $R_{*}(X)v\in W_{m+2}$ if and only if $R_{*}(H)R_{*}(X)v=(m+2)R_{*}(X)v$ .

13.40 We know that $R_{*}(X)R_{*}(H)v=R_{*}(X)mv=mR_{*}(X)v$ , but we can't just commute $R_{*}(H)$ past $R_{*}(X)$ . However, we know that $[H,X]=2X$ , and since $R_{*}$ is a Lie algebra homomorphism we have $[R_{*}(H),R_{*}(X)]=2R_{*}(X)$ .

15.00 Therefore
$R_{*}(H)R_{*}(X)v=R_{*}(X)R_{*}(H)v+2R_{*}(X)v=(m+2)R_{*}(X)v,$ as required.

Pre-class exercise

Exercise:

Suppose that $R\colon SU(2)\to GL(V)$ is a representation with weight decomposition $V=\bigoplus W_{m}$ . Show that $R_{*}^{\mathbf{C}}(Y)$ sends $W_{m}$ to $W_{m-2}$ .