So far we have seen that, given a complex representation R from S U 2 to G L V, we get:
a (real linear) representation R star from little s u 2 to little g l V of the real Lie algebra little s u 2
a (complex linear) representation R star superscript C from little s l 2 C to little g l V of its complexification little s l 2 C equals little s u 2 tensor C.
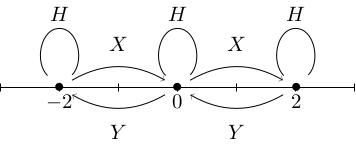
Define the basis H equals the diagonal matrix 1, -1, X is the 2-by-2 matrix 0, 1, 0, 0 and Y is the 2-by-2 matrix 0, 0, 1, 0 of little s u 2. We saw that V splits as a direct sum of weight spaces W_m where W_m is the eigenspace of R star superscript C of H with eigenvalue m and saw that X and Y act on weight spaces as follows:
X takes vectors in W_m to vectors in W_{m+2},
Y takes vectors in W_m to vectors in W_(m minus 2).
We will usually omit the superscript C from R star superscript C and actually, we'll usually omit the R star altogether.
In this video, I want to see how this actually works in practice for the example Sym 2 C 2. But first, we will need to understand how Lie algebras act on symmetric powers and, more generally, tensor products.
Recall that R tensor square of g applied to v_1 tensor v_2 equals R of g applied to v_1 tensor R of g applied to v_2. What is the Lie algebra representation corresponding to this? In other words, what is (R tensor squared) star?
If R from big G to G L V is a representation and X is in little g (this is not necessarily the X in little s l 2 C) we have (R to the nth tensor power) star of X applied to v_1 tensor dot dot dot tensor v_n equals R star X applied to v_1, tensor v_2 tensor dot dot dot tensor v_n, plus v_1 tensor R star X applied to v_2, tensor dot dot dot tensor v_n, plus dot dot dot, plus v_1 tensor dot dot dot tensor R star X applied to v_n In other words, we use the "Leibniz/product rule".
For now, we will assume this lemma, work out the example and then justify the lemma.
Let V be Sym 2 of C 2. If e_1 and e_2 form a basis for C 2 then e_1 squared (which equals e_1 tensor e_1), e_1 e_2 (which equals e_1 tensor e_2 plus e_2 tensor e_1) and e_2 squared (which equals e_2 tensor e_2) form a basis for Sym 2 C 2. The Lie algebra elements H, X and Y act on e_1 and e_2 as follows:
Since H is diagonal 1, -1, we have H e_1 = e_1, H e_2 equals minus e_2,
Since X equals 0, 1, 0, 0, we have X e_1 = 0, X e_2 = e_1,
Since Y equals 0, 0, 1, 0, we have Y e_1 = e_2, Y e_2 = 0.
Sym 2 H therefore sends e_1 squared equals e_1 tensor e_1 to (H e_1) tensor e_1 plus e_1 tensor (H e_1), which equals 2 e_1 squared by the product rule. Similarly, Sym 2 H of e_1 e_2 equals (H e_1) e_2 plus e_1 (H e_2), which equals e_1 e_2 minus e_1 e_2, which equals 0, and Sym 2 H of e_2 squared equals minus 2 e_2 squared. The weight spaces, that is the eigenspaces of H, are spanned by e_1 squared (weight 2), e_1 e_2 (weight 0) and e_2 squared (weight minus 2).
Let's compute Sym 2 X:
Sym 2 X of e_1 squared equals X e_1 times e_1 plus e_1 times X e_1, which equals 0.
Sym 2 X of e_1 e_2 equals X e_1 times e_2 plus e_1 times X e_2, which equals e_1 squared.
Sym 2 X of e_2 squared equals X e_2 times e_2 plus e_2 times X e_2, which equals 2 e_2 e_2.
Notice that in this last example we used the fact that e_1 e_2 = e_2 e_1 (which holds because it's a symmetric tensor).
In terms of our weight diagram, we can see that Sym 2 X is taking e_2 squared in W_(minus 2) to 2 e_1 e_2 in W_0 (increasing the weight by 2) and e_1 e_2 in W_0 to e_1 squared in W_2 (again, increasing the weight by 2). Finally, it takes e_1 squared in W_2 to 0 in W_4 (necessarily, since W_4 = 0).
It's an exercise to calculate Sym 2 Y.
We still need to prove that (R to the nth tensor power) star can be evaluated using the Leibniz rule, as stated in the lemma.
We have R to the nth tensor power of exp t X equals exp of (t (R to the nth tensor power) star X) by our usual formula for Lie algebra representations.
Let's apply both sides to v_1 tensor dot dot dot tensor v_n and expand both sides in powers of t. The right-hand side is the identity plus t (R to the nth tensor power) star X plus terms of order t squared) applied to v_1 tensor dot dot dot tensor v_n, which equals v_1 tensor dot dot dot tensor v_n plus t (R to the nth tensor power) star applied to v_1 tensor dot dot dot tensor v_n, plus terms of order t squared. The left-hand side is R of exp t X v_1 tensor dot dot dot tensor R exp t X v_n.
We have R exp t X v_i equals (the identity plus t R star X plus higher order terms) applied to v_i, which equals v_i plus t R star X v_i plus higher order terms, so multiplying out the brackets, the left-hand side becomes: v_1 tensor dot dot dot tensor v_n, plus t times, (R star X v_1) tensor v_2 tensor dot dot dot tensor v_n, plus v_1 tensor R star X v_2 tensor dot dot dot tensor v_n, plus dot dot dot, plus v_1 tensor dot dot dot tensor R star X v_n, plus higher order terms.
By comparing the terms of order t, we get the desired formula for (R to the nth tensor power) star X.
Compute the action of \mathrm{Sym}^2(Y) on the basis e_1^2, e_1e_2, e_2^2.