Take the subspace U spanned by v, Y v, Y squared v, up to Y to the n v. I claim that U inside V is a subrepresentation.
Classifying SU(2) representations
Review
We have seen that for every complex representation R from S U 2 to G L V we get a Lie algebra representation R star superscript C from little s u 2 to little g l V (by complexifying R star; we'll usually omit the superscript C and sometimes even the R star). We have a basis H equals 1, 0, 0, minus 1; X equals 0, 1, 0, 0; and Y equals 0, 0, 1, 0 of little s l 2 C which satisfy the commutator relations H bracket X equals 2 X, H bracket Y equals minus 2 Y and X bracket Y equals H.
We've seen that V is the direct sum of subspaces W_m where W_m is the m-eigenspace of H, and that X sends W_m to W_(m+2) and Y sends W_m to W_(m minus 2). The spaces W_m are called weight spaces and the ms are called weights.
We depict this by drawing a weight diagram with a blob at each integer point m for which W_m is nonzero (and somehow indicating the dimension of W_m).
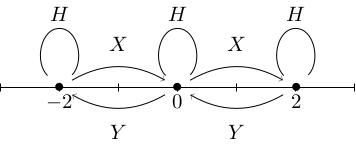
Highest weight vectors
Pick a vector v in W_m where m is the weight that is furthest to the right in the diagram. Such a weight exists because V is finite-dimensional. Act on v using the matrices R star X, R star Y, and R star H (which we're now calling X, Y and H for brevity). Because V is a representation, all vectors we obtain in this way are again in V.
X v = 0 because X v is in W_(m plus 2), which is zero, so we may as well start by applying Y a bunch of times to obtain the following elements: Y to the n v, Y to the n minus 1 v, dot dot dot, Y squared v, Y v, v Here, I've ordered these elements by increasing weight: each time we apply Y we decrease weight by 2, so Y to the k v in W_(m minus 2 k). Also, let's define n to be the biggest power of Y we can apply before we get zero, that is: Y to the n v is nonzero but Y to the n plus 1 v equals 0. (Again this n is guaranteed to exist because V is finite-dimensional).
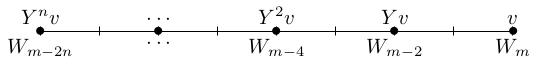
If V is irreducible then this implies V = U. In other words, any irreducible representation of SU(2) has a weight diagram that looks like a string of dots spaced out in twos (W_(m minus 2 n), dot dot dot, W_(m minus 4), W_(m minus 2), W_m with each weight space 1-dimensional (spanned by Y to the k v for some k).
To check that U is a subrepresentation, we need to check that if little u is in U and we apply X, Y or H to little u then the result is still in U. We will check this for little u running over the basis v, Y v, Y squared v, dot dot dot, Y to the n v.
If we apply Y to Y to the k v then we get Y to the k plus 1 v, and all these vectors are still in U.
If we apply H to Y to the k v we get (m minus 2 k) times Y to the k v because Y to the k v is in W_(m minus 2 k). Again, this stays in the subrepresentation U.
If we apply X, there is a formula which we will prove separately: X Y to the k v equals (m plus 1 minus k), times k, times Y to the k minus 1 v This implies the lemma because it shows X Y to the k v is in U.
The formula
X Y to the k v equals (m plus 1 minus k), times k, times Y to the k minus 1 v.
Consequences of the formula
We'll prove the formula in a moment, but first here are some remarks.
The formula makes sense because X increases weight by 2 and Y to the k v is in W_(m minus 2 k) while Y to the k minus 1 v is in W_(m minus 2 k plus 2).
The formula tells us that the irreducible representation with highest weight m is completely determined up to isomorphism by m (i.e. there's a unique irrep with highest weight m up to isomorphism). This is because we know how all the matrices R star X, R star Y, R star H act on the basis v, Y v, Y squared v, dot dot dot, Y to the n v:
-
Y applied to Y to the k v equals Y to the k plus 1 v
-
H applied to Y to the k v equals (m minus 2 k) times Y to the k v
-
X applied to Y to the k v equals (m plus 1 minus k) times k times Y to the k minus 1 v.
The only choice we have is picking the vector v, but different vs differ only by a scale factor as W_m is 1-dimensional, and this just amounts to changing our whole basis Y to the k v by a scale factor.
We can now deduce that Sym 2 C 2 is isomorphic to the representation R of g M_v equals g M_v g inverse: we've seen both of these have the same weight diagram.
The formula also tells us that n (the biggest power of Y for which Y to the n v is nonzero but Y to the n plus 1 v equals 0) is equal to m. Therefore the weights in our representations go from m down to m minus 2 n, which equals minus m.
To see why n = m, note that X Y to the n plus 1 v equals 0, equals (m plus 1 minus n minus 1) times (n plus 1) times Y to the n v but Y to the n v is nonzero and n plus 1 is nonzero, so m plus 1 minus n minus 1 equals 0 and hence n = m.
Proof of formula
We now prove the formula X Y to the k v equals (m plus 1 minus k), times k, times Y to the k minus 1 v. We prove it by induction on k.
For k = 0, X v = 0 and (m plus 1 minus k) times k times Y to the k minus 1 v equals 0, so both sides agree.
Suppose it's true for all numbers strictly less than k. We know that X Y minus Y X equals X bracket Y equals H. Since R star superscript C is a representation of Lie algebras this formula is still true if we stick R star superscript C in front of everything (which is good, since we're omitting mention of R star superscript C from the formulae). Let's apply X Y - Y X = H to Y to the k minus 1 v: X Y to the k v minus Y X Y to the k minus 1 v equals H Y to the k minus 1 v.
Therefore X Y to the k v equals Y X Y to the k minus 1 v, plus H Y to the k minus 1 v. Using our formula to evaluate X Y to the k minus 1 v and the fact that Y to the k minus 1 v is in W_(m minus 2 k plus 2), we get X Y to the k v equals (m plus 1 minus k plus 1) times (k minus 1) Y to the k minus 1, plus (m minus 2 k plus 2) Y to the k minus 1 v, which simplifies to give our formula (exercise!).
Once again, the bracket relations in little s l 2 C have played a crucial role in the proof.
Summary
With this formula in hand, we have now established these nice facts:
-
the weight diagrams of SU(2) representations are symmetric about the origin
-
there's a unique irrep with highest weight m, whose weight diagram has 1-dimensional weight spaces with weights minus m, minus m plus 2, minus m plus 4, dot dot dot, up to m (spaced out by 2, starting at minus m and ending at m).
Pre-class exercise
Check that X Y to the k v equals (m plus 1 minus k plus 1) times (k minus 1) Y to the k minus 1, plus (m minus 2 k plus 2) Y to the k minus 1 v, simplifies to give X Y to the k v equals (m plus 1 minus k), times k, times Y to the k minus 1 v.