Any irrep of SU(2) is isomorphic to Sym n of C 2 for some n equals 0, 1, 2, etc and this has weight diagram:
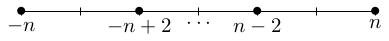
We have now established the following theorem.
Any irrep of SU(2) is isomorphic to Sym n of C 2 for some n equals 0, 1, 2, etc and this has weight diagram:
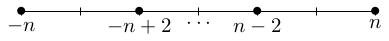
There is also a complete reducibility theorem:
Any finite-dimensional SU(2) representation splits as a direct sum of irreps.
This is proved in exactly the same way as for representations of U(1) once you understand how to integrate (average) over the group SU(2). Instead of talking about that, I will work through some examples, decomposing representations into irreducibles.
Consider the standard representation C 2 tensored with itself: C 2 tensor C 2. This will turn out to have the following weight diagram:

In other words, there are 1-dimensional weight spaces with weights 2 and minus 2 and a 2-dimensional weight space in weight 0.
Inside this diagram, you can see the weight diagram of Sym 2 C 2 as a subdiagram. When you remove this subdiagram what's left is the weight diagram of the trivial 1-dimensional representation.

This will allow us to deduce that C 2 tensor C 2 is isomorphic to Sym 2 C 2 direct sum the trivial representation C.
A basis for C 2 tensor C 2 is given by e_1 tensor e_1, e_1 tensor e_2, e_2 tensor e_1 and e_2 tensor e_2 (where e_1, e_2 is the standard basis for C 2. We have H e_1 equals e_1, H e_2 equals minus e_2 Because H lives in the Lie algebra, we evaluate H of x tensor y using the product rule: H of (e_1 tensor e_1) equals (H of e_1) tensor e_1 plus e_1 tensor (H of e_1), which equals 2 e_1 tensor e_1
Therefore e_1 tensor e_1 is an eigenvector for H with eigenvalue 2, so it lives in the weight space W_2. Similarly we get H of e_1 tensor e_2) equals e_1 tensor e_2 minus e_1 tensor e_2 equals 0, and similarly for H of e_2 tensor e_1 which give us the 2-dimensional weight space W_0 and H of e_2 tensor e_2 equals minus 2 e_2 tensor e_2 which gives the weight space W_(minus 2). So our weight spaces are: W_(minus 2) spanned by e_2 tensor e_2, W_0 spanned by e_1 tensor e_2 and e_2 tensor e_1, and W_2 spanned by e_2 tensor e_2.
Following the procedure we used in proving the classification theorem, we pick a highest weight vector v equals e_1 tensor e_1 and use Y equals 0, 0, 1, 0 to generate a subrepresentation spanned by: v, Y v, and Y squared v These three vectors live in the weight spaces W_2, W_0 and W_(minus 2) respectively, and give a subrepresentation U isomorphic to Sym 2 C 2 (because it has the right weight diagram).
There is an invariant Hermitian inner product on the representation, and we take the orthogonal complement U perp to get a complementary subrepresentation. Since this complement is 1-dimensional, it must be isomorphic to the trivial 1-dimensional representation (the only irrep of this dimension).
We deduce that C 2 tensor C 2 is isomorphic to Sym 2 C 2 direct sum C. This should not be a surprise, because Sym 2 C 2 was defined to be a subrepresentation of C 2 tensor C 2, in fact it was defined to be the subrepresentation spanned by the symmetric tensors e_1 tensor e_1, e_1 tensor e_2 plus e_2 tensor e_1 and e_2 tensor e_2.
Let's check that this is what we are getting. Since Y equals 0, 0, 1, 0 we have Y e_1 = e_2 and Y e_2 = 0. If v equals e_1 tensor e_1 then Y v equals (Y e_1) tensor e_1 plus e_1 tensor Y e_1, which equals e_2 tensor e_1 plus e_1 tensor e_2, and Y squared v equals (Y e_2) tensor e_1 plus e_1 tensor (Y e_1) plus Y e_1 tensor e_2 plus e_2 tensor (Y e_1), which equals 2 e_2 tensor e_2 so we get precisely that U equals Sym 2 of C 2 on the nose.
The complementary subrepresentation turns out to be spanned by the antisymmetric tensor e_1 tensor e_2 minus e_2 tensor e_2, which spans the exterior square Lambda 2 C 2. It's an exercise to check that this antisymmetric tensor does span a subrepresentation (i.e. it is fixed by the action of SU(2)).
Let's figure out the decomposition of Sym 2 Sym 2 C 2. We know that Sym 2 C 2 is spanned by alpha equals e_1 squared, beta equals e_1 e_2 and gamma equals e_2 squared. In the same way we can think of Sym 2 C 2 as quadratic polynomials in e_1, e_2, we can think of Sym 2 Sym 2 C 2 as quadratic polynomials in \alpha, \beta, and \gamma. It therefore has a basis alpha squared, alpha beta, alpha gamma, beta squared, beta gamma, and gamma squared.
Let's calculate the weight space decomposition. We know that H alpha equals 2 alpha, H beta equals 0 and H gamma equals minus 2 gamma, so (using the product rule) we have H of alpha squared equals (H alpha) times alpha plus alpha times (H alpha), which equals 4 alpha squared H (alpha beta) equals (H alpha) times beta plus alpha times (H beta) equals 2 alpha beta H alpha gamma equals H beta squared equals 0, H beta gamma equals minus 2 beta gamma, and H gamma squared equals minus 4 gamma squared. The weight space decomposition is therefore: W_(minus 4) spanned by gamma squared, W_(minus 2) spanned by beta gamma, W_0 spanned by beta squared and alpha gamma, W_2 spanned by alpha beta, and W_4 spanned by alpha squared. with weight diagram

From this you can see that Sym 2 Sym 2 C 2 equals Sym 4 C 2 direct sum C The argument is exactly as before: you pick a highest weight vector like v equals alpha squared and you generate a highest weight subrepresentation U spanned by v, Y v, Y squared v, Y cubed v, Y to the 4 v, which is isomorphic to Sym 4 C 2 by the classification theorem. Then you take the orthogonal complement of U with respect to an invariant Hermitian inner product and you get a complementary subrepresentation whose weight diagram is obtained from the weight diagram of Sym 2 Sym 2 C 2 by stripping off the weight diagram of U.
The trivial complementary subrepresentation has to be spanned by some combination of beta squared and alpha gamma as these span the 0-weight space. In this case, I claim that the trivial complementary subrepresentation is spanned by beta squared minus alpha gamma (it will be an exercise to check this).
Compute the weight diagrams and decomposition of \mathrm{Sym}^k(\CC^2)\otimes\mathrm{Sym}^\ell(\CC^2) for a few different values of k and \ell and see if you can formulate a conjecture as to what the answer should be in general.