Root vectors acting on weight spaces

Review

0.00 Given a representation $R\colon SU(3)\to GL(V)$ , we have seen that $V=\bigoplus W_{k,\ell}$ where $k,\ell\in\mathbf{Z}$ and $W_{k,\ell}=\left\{v\in V\ :\ R\begin{pmatrix}e^{i\theta_{1}}&0&0\\ 0&e^{i\theta_{2}}&0\\ 0&0&e^{-i(\theta_{1}+\theta_{2})}\end{pmatrix}v=e^{i(k\theta_{1}+\ell\theta_{3% })}v\right\}$ or equivalently $W_{k,\ell}=\left\{v\in V\ :\ R_{*}^{\mathbf{C}}\begin{pmatrix}\theta_{1}&0&0\\ 0&\theta_{2}&0\\ 0&0&-(\theta_{1}+\theta_{2})\end{pmatrix}v=(k\theta_{1}+\ell\theta_{3})v\right\}$

1.20 Remember that $\begin{pmatrix}\theta_{1}&0&0\\ 0&\theta_{2}&0\\ 0&0&-(\theta_{1}+\theta_{2})\end{pmatrix}$ isn't in $\mathfrak{su}(3)$ , rather it's in $\mathfrak{sl}(3,\mathbf{C})=\mathfrak{su}(3)\otimes\mathbf{C}$ , which is why we're using $R_{*}^{\mathbf{C}}$ .

We were drawing the weights $(k,\ell)$ on a triangular lattice. For example, the weight diagram for the adjoint representation was:

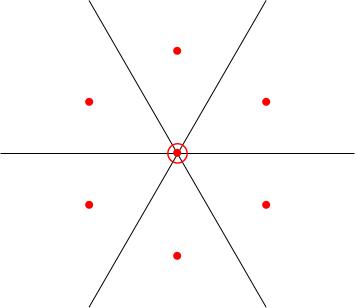
Weight diagram of the adjoint representation of SU(3) on a triangular lattice

Remark:

2.10 We will change notation slightly and write $W_{k,\ell}=W_{\lambda}$ where $\lambda(\theta)=k\theta_{1}+\ell\theta_{2}$ . Bundling the two integers together in this way will make life easier in future (e.g. when we have more than two integer weights).

Definition:

3.00 Define $L_{1}(\theta)=\theta_{1}$ , $L_{2}(\theta)=\theta_{2})$ , $L_{3}(\theta)=\theta_{3}=-\theta_{1}-\theta_{2}$ . These are the $\lambda$ s corresponding to $(k,\ell)=(1,0),(0,1),(-1,-1)$ respectively.

With this notation, the weights of the standard representation are $L_{1},L_{2},L_{3}$ and the weights of the adjoint representation are $L_{i}-L_{j}$ because $\mathrm{ad}(H_{\theta})E_{ij}=(\theta_{i}-\theta_{j})E_{ij}=(L_{i}-L_{j})(% \theta)E_{ij}.$

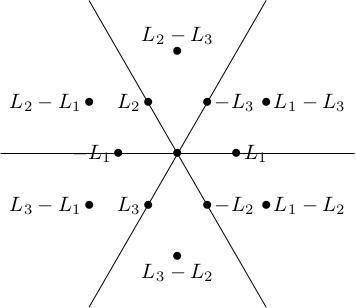
Weights L_i and L_i - L_j on the triangular lattice

The analogue of X and Y

Statement

5.55 For $\mathfrak{sl}(2,\mathbf{C})$ , the adjoint representation has weight spaces $W_{-2}=\mathbf{C}\cdot Y$ , $W_{0}=\mathbf{C}\cdot H$ and $W_{2}=\mathbf{C}\cdot X$ . The elements $X$ and $Y$ played an important role in studying the representations of $SU(2)$ : $X$ moved vectors from weight spaces with weight $k$ to weight spaces with weight $k+2$ and $Y$ moved them back again.

6.50 The analogue for $SU(3)$ will be to see how the weight vectors $E_{ij}\in\mathfrak{sl}(3,\mathbf{C})$ of the adjoint representation act on the weight spaces of another representation.

Lemma:

7.10 Given a complex representation $R\colon SU(3)\to GL(V)$ , $R_{*}^{\mathbf{C}}(E_{ij})$ sends $W_{\lambda}$ to $W_{\lambda+L_{i}-L_{j}}$ .

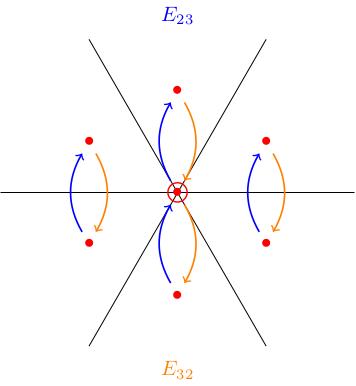
Example: Adjoint representation

We illustrate the lemma in the figures below, showing how the matrices $R_{*}^{\mathbf{C}}(E_{ij})$ act in the adjoint representation. For example $R_{*}^{\mathbf{C}}(E_{13})$ and $R_{*}^{\mathbf{C}}(E_{31})$ translate weight spaces forwards and backwards along the $L_{1}-L_{3}$ direction.

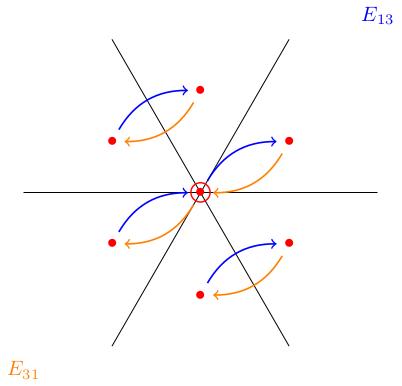
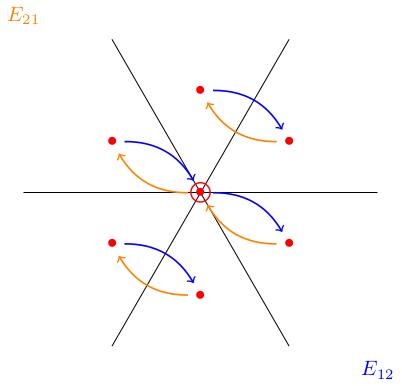
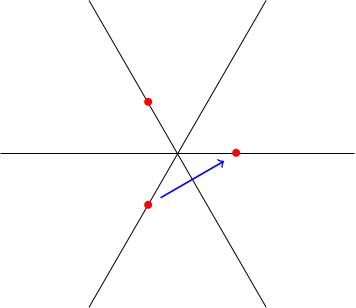
Example: standard representation

11.55 The figure below shows the standard representation. There are three weights $L_{1},L_{2},L_{3}$ . Let's see how $E_{13}=\begin{pmatrix}0&0&1\\ 0&0&0\\ 0&0&0\end{pmatrix}$ acts. It sends $e_{1}\in W_{L_{1}}$ and $e_{2}\in W_{L_{2}}$ to zero and it sends $e_{3}\in W_{L_{3}}$ to $e_{1}\in W_{L_{1}}$ . Correspondingly, we draw an arrow in the $L_{3}-L_{1}$ -direction in the weight diagram, as dictated by the lemma.

Remark:

13.20 We know that $E_{13}$ sends $W_{L_{1}}$ to $W_{2L_{1}-L_{3}}$ by the lemma, but $W_{2L_{1}-L_{3}}=0$ which is why $E_{13}e_{1}=0$ . In terms of the figure, the vector $L_{1}-L_{3}$ starting at $L_{1}$ ends at a lattice point which is not in the weight diagram.

The action of E_{1 3} on the weight spaces of the standard representation

Proof of lemma

13.40 If $v\in W_{\lambda}$ then we need to show $R_{*}^{\mathbf{C}}(E_{ij})v\in W_{\lambda+L_{i}-L_{j}}$ .

We have $v\in W_{\lambda}$ if and only if $R^{\mathbf{C}}_{*}(H_{\theta})v=\lambda(\theta)v$ .

We have $R_{*}^{\mathbf{C}}(E_{ij})v\in W_{\lambda+L_{i}-L_{j}}$ if and only if $R^{\mathbf{C}}_{*}(H_{\theta})R_{*}^{\mathbf{C}}(E_{ij})v=(\lambda(\theta)+% \theta_{i}-\theta_{j})R_{*}^{\mathbf{C}}(E_{ij})v$ .

15.10 We have $[H_{\theta},E_{ij}]=\mathrm{ad}(H_{\theta})E_{ij}=(\theta_{i}-\theta_{j})E_{ij}$ , because $E_{ij}\in W_{L_{i}-L_{j}}^{\mathrm{ad}}$ . Applying $R_{*}^{\mathbf{C}}$ we get $R_{*}^{\mathbf{C}}[H_{\theta},E_{ij}]=[R_{*}^{\mathbf{C}}(H_{\theta}),R_{*}^{% \mathbf{C}}(E_{ij})]=(\theta_{i}-\theta_{j})R_{*}^{\mathbf{C}}(E_{ij}).$

16.40 Therefore $R_{*}^{\mathbf{C}}(H_{\theta})R_{*}^{\mathbf{C}}(E_{ij})v=R_{*}^{\mathbf{C}}(E% _{ij})R_{*}^{\mathbf{C}}(H_{\theta})v+(\theta_{i}-\theta_{j})R_{*}^{\mathbf{C}% }(E_{ij})v.$

17.50 Since $v\in W_{\lambda}$ , we have $R_{*}^{\mathbf{C}}(H_{\theta})v=\lambda(\theta)v$ , so $R_{*}^{\mathbf{C}}(H_{\theta})R_{*}^{\mathbf{C}}(E_{ij})v=(\lambda(\theta)+% \theta_{i}-\theta_{j})R_{*}^{\mathbf{C}}(E_{ij})v.$ This shows that $R_{*}^{\mathbf{C}}(E_{ij})v\in W_{\lambda+L_{i}-L_{j}}$ as required.

Remark:

19.10 We have used two crucial things:

$R_{*}^{\mathbf{C}}$ is a representation
$\mathrm{ad}(H_{\theta})E_{ij}=(\theta_{i}-\theta_{j})E_{ij}$ , in other words, $E_{ij}\in W^{\mathrm{ad}}_{L_{i}-L_{j}}$ .

The same proof shows more generally that if $X\in\mathfrak{g}$ is a weight vector of the adjoint representation (root vector) with weight (root) $\alpha$ then $X$ sends weight vectors in $W_{\lambda}$ (for any representation) to weight vectors in $W_{\lambda+\alpha}$ .

Pre-class exercises

Exercise:

What do you think the weight diagram of the standard 4-dimensional representation of $SU(4)$ would look like? How do you think the matrices $E_{ij}$ act?