Adjoint representation

0.00 Before we classify the representations of $SU(3)$ , I want to introduce a representation which makes sense for any Lie group, the adjoint representation, and study it for $SU(3)$ .

Definition:

0.20 Given a matrix group $G$ with Lie algebra $\mathfrak{g}$ , the adjoint representation is the homomorphism $\mathrm{Ad}\colon G\to GL(\mathfrak{g})$ defined by $\mathrm{Ad}(g)X=gXg^{-1}.$ In other words:

the vector space on which we're acting is $\mathfrak{g}$ ,
$\mathrm{Ad}(g)$ is a linear map $\mathfrak{g}\to\mathfrak{g}$ .

1.35 It is an exercise to check that this is a representation, but I will explain why it is well-defined, in other words why is $gXg^{-1}\in\mathfrak{g}$ when $X\in\mathfrak{g}$ and $g\in G$ .

Lemma:

If $X\in\mathfrak{g}$ and $g\in G$ then $gXg^{-1}\in\mathfrak{g}$ .

Proof:

2.10 We need to show that for all $t\in\mathbf{R}$ , $\exp(tgXg^{-1})\in G$ . As a power series, this is: $\exp(tgXg^{-1})=I+tgXg^{-1}+\frac{1}{2}t^{2}gXg^{-1}gXg^{-1}+\cdots,$

2.50 All of the $g^{-1}g$ s sandwiched between the $X$ s cancel and we get $I+tgXg^{-1}+\frac{1}{2}t^{2}gX^{2}g^{-1}+\cdots=g\exp(tX)g^{-1}.$

3.25 Since $g\in G$ , $g^{-1}\in G$ and $\exp(tX)\in G$ for all $t$ , we see that this product is in $G$ for all $t$ , which proves the lemma.

Definition:

3.55 The induced map on Lie algebras is $\mathrm{ad}=\mathrm{Ad}_{*}\colon\mathfrak{g}\to\mathfrak{gl}(\mathfrak{g})$ . (I apologise for the profusion of g's playing different notational roles).

Let's calculate $\mathrm{ad}(X)$ for some $X\in\mathfrak{g}$ . This is a linear map $\mathfrak{g}\to\mathfrak{g}$ , so let's apply it to some $Y\in\mathfrak{g}$ : $\mathrm{ad}(X)Y=\left.\frac{d}{dt}\right|_{t=0}(\mathrm{Ad}(\exp(tX))Y)$ (This is how we calculate $R_{*}$ for any representation $R$ : it follows by differentiating $R(\exp(tX))=\exp(tR_{*}X)$ with respect to $t$ ). This gives: $\mathrm{ad}(X)Y=\left.\frac{d}{dt}\right|_{t=0}(\exp(tX)Y\exp(-tX))=(X\exp(tX)% Y\exp(-tX)-\exp(tX)YX\exp(-tX))|_{t=0}=XY-YX.$

6.00 In other words, $\mathrm{ad}(X)Y=[X,Y].$ Note that this makes sense even without reference to $G$ .

Exercise:

Since $\mathrm{ad}=\mathrm{Ad}_{*}$ we know already that it's a representation of Lie algebras, but it's possible to prove it directly from the axioms of a Lie algebra without reference to the group $G$ i.e. that $\mathrm{ad}([X,Y])Z=\mathrm{ad}(X)\mathrm{ad}(Y)Z-\mathrm{ad}(Y)\mathrm{ad}(X)Z$ for all $X,Y,Z\in\mathfrak{g}$ . Do this!

Example: sl(2,C)

7.40 Recall that we have a basis $H, X, Y$ for $\mathfrak{sl}(2,\mathbf{C})$ . Let's compute $\mathrm{ad}(H)$ with respect to this basis.

8.05 $\mathrm{ad}(H)$ sends:

$H$ to $[H,H]=0$ ,
$X$ to $[H,X]=2X$ ,
$Y$ to $[H,Y]=-2Y$ ,

so $\mathrm{ad}(H)=\begin{pmatrix}0&0&0\\ 0&2&0\\ 0&0&-2\end{pmatrix}$ with respect to this basis.

8.50 In fact, the action of $H$ on a representation tells us the weights, so we see that the weights of the adjoint representation are $-2,0,2$ . In particular, the adjoint representation is isomorphic to $\mathrm{Sym}^{2}(\mathbf{C}^{2})$ .

It's an exercise to compute $\mathrm{ad}(X)$ and $\mathrm{ad}(Y)$ .

Example: sl(3,C)

9.35 Let's find a basis of $\mathfrak{sl}(3,\mathbf{C})$ . Define $E_{ij}$ to be the matrix with zeros everywhere except in position $i, j$ where there is a 1, e.g. $E_{12}=\begin{pmatrix}0&1&0\\ 0&0&0\\ 0&0&0\end{pmatrix}.$ There are 6 such matrices with $i\neq j$ . Together with $H_{13}=\begin{pmatrix}1&0&0\\ 0&0&0\\ 0&0&-1\end{pmatrix},\quad H_{23}=\begin{pmatrix}0&0&0\\ 0&1&0\\ 0&0&-1\end{pmatrix}$ this gives us a basis of $\mathfrak{sl}(3,\mathbf{C})$ ; in other words, any tracefree complex matrix can be written as a complex linear combination of these 8 (it's an 8-dimensional Lie algebra).

11.15 More generally, we will write $H_{\theta}=\begin{pmatrix}\theta_{1}&0&0\\ 0&\theta_{2}&0\\ 0&0&\theta_{3}\end{pmatrix}\in\mathfrak{sl}(3,\mathbf{C})$ where $\theta=(\theta_{1},\theta_{2},\theta_{3})$ is a vector satisfying $\theta_{1}+\theta_{2}+\theta_{3}=0.$ I want to compute $\mathrm{ad}(H_{\theta})$ .

12.05 We have $\mathrm{ad}(H_{\theta})H_{ij}=0$ because the $H$ -matrices are all diagonal (and hence all commute with one another). This means that $H_{13}$ and $H_{23}$ are contained in the zero-weight space of the adjoint representation. This is because $\exp(iH_{\theta})=\begin{pmatrix}e^{i\theta_{1}}&0&0\\ 0&e^{i\theta_{2}}&0\\ 0&0&e^{-i(\theta_{1}+\theta_{2})}\end{pmatrix}$ , so the eigenvalues of $H_{\theta}$ tell us the weights of the representation.

13.05 It turns out that $\mathrm{ad}(H_{\theta})E_{ij}=(\theta_{i}-\theta_{j})E_{ij}$ . For example: $[H_{\theta},E_{12}]=\left[\begin{pmatrix}\theta_{1}&0&0\\ 0&\theta_{2}&0\\ 0&0&\theta_{3}\end{pmatrix},\begin{pmatrix}0&1&0\\ 0&0&0\\ 0&0&0\end{pmatrix}\right]=\begin{pmatrix}0&\theta_{1}&0\\ 0&0&0\\ 0&0&0\end{pmatrix}-\begin{pmatrix}0&\theta_{2}&0\\ 0&0&0\\ 0&0&0\end{pmatrix}.$

14.15 Let's figure out the weights of the adjoint representation. If $v\in W_{k,\ell}$ then we have $\exp(i\mathrm{ad}(H_{\theta}))v=e^{i(k\theta_{1}+\ell\theta_{2})}v$ , so $\mathrm{ad}(H_{\theta})v=(k\theta_{1}+\ell\theta_{2})v$ . For example, $E_{12}$ satisies $\mathrm{ad}(H_{\theta})E_{12}=(\theta_{1}-\theta_{2})E_{12}$ , so $E_{12}\in W_{1,-1}$ .

15.45 Similarly, we get $\mathrm{ad}(H_{\theta})E_{13}=(\theta_{1}-\theta_{3})E_{13}=(2\theta_{1}+% \theta_{2})E_{13}$ , so $E_{13}\in W_{2,1}$ .

Exercise:

The other weight space that occur are: $E_{12}\in W_{1,-1},\ E_{21}\in W_{-1,1},\ E_{13}\in W_{2,1},\ E_{31}\in W_{-2,% -1},\ E_{23}\in W_{1,2},\ E_{32}\in W_{-1,-2}$ and the weight diagram is the hexagon shown in the figure below.

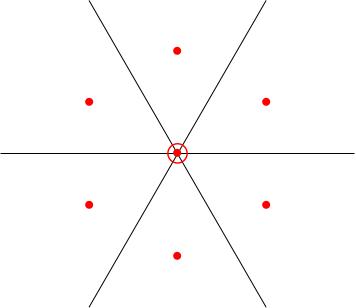
The weight diagram of the adjoint representation of sl 3 C

17.00 Note that the zero-weight space is spanned by $H_{13}$ and $H_{23}$ , which means it's 2-dimensional. We've denoted this by putting a circle around the dot at the origin in the weight diagram.

Remark:

18.00 The weight space decomposition of the adjoint representation is sufficiently important to warrant its own name: it's called the root space decomposition. The weights that occur are called roots and the weight diagram is called a root diagram.

Pre-class exercise

Exercise:

The matrices $E_{ij}$ inhabit the following weight spaces: $E_{12}\in W_{1,-1},\ E_{21}\in W_{-1,1},\ E_{13}\in W_{2,1},\ E_{31}\in W_{-2,% -1},\ E_{23}\in W_{1,2},\ E_{32}\in W_{-1,-2}$ and the weight diagram is the hexagon shown above.