The Weyl group of SU(3)

Review

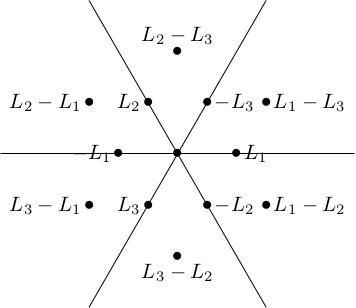
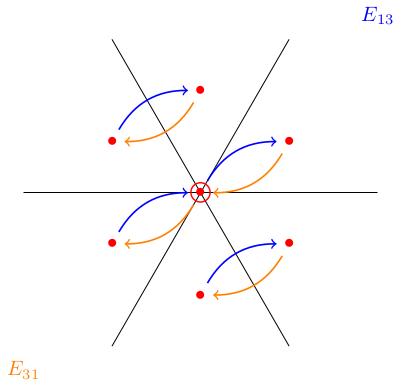
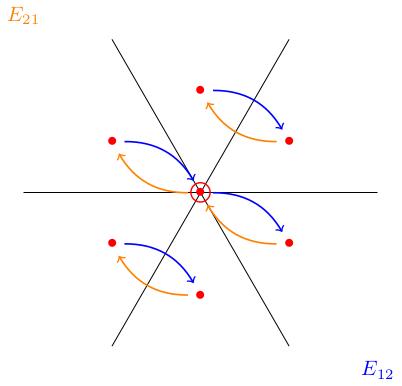
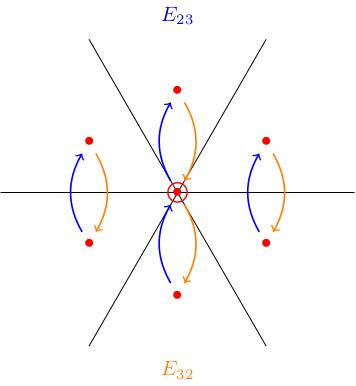
0.00 Last time, we introduced special names for some of the weights of an $SU(3)$ -representation: we set $L_{1}(\theta)=\theta_{1}$ , $L_{2}(\theta)=\theta_{2})$ , $L_{3}(\theta)=\theta_{3}=-\theta_{1}-\theta_{2}$ . The roots (weight of the adjoint representation) are then $L_{i}-L_{j}$ , with the root space spanned by $E_{ij}\in W_{L_{i}-L_{j}}$ . We discussed how the root vectors $E_{ij}\in\mathfrak{sl}(3,\mathbf{C})$ act on the weight spaces of a complex $SU(3)$ -representation: $E_{ij}\colon W_{\lambda}\to W_{\lambda+L_{i}-L_{j}}.$ This is all illustrated in the following figures.

Weights L_i and L_i - L_j on the triangular lattice

Lemma:

1.20 $E_{ij}$ , $E_{ji}$ and $H_{ij}=[E_{ij},E_{ji}]$ span a subalgebra of $\mathfrak{sl}(3,\mathbf{C})$ isomorphic to $\mathfrak{sl}(2,\mathbf{C})$ .

Proof:

The matrices are simply obtained from $X, Y, H$ by adding a row and column of zeros in position $k$ where $i, j, k$ is a permutation of $1,2,3$ . For example, $E_{12}=\begin{pmatrix}0&1&0\\ 0&0&0\\ 0&0&0\end{pmatrix},\ E_{21}=\begin{pmatrix}0&0&0\\ 1&0&0\\ 0&0&0\end{pmatrix},\ H_{12}=\begin{pmatrix}1&0&0\\ 0&-1&0\\ 0&0&0\end{pmatrix}$ and you get $X, Y, H$ by deleting row and column 3 from these three matrices.

This tells us that $E_{ij}$ , $E_{ji}$ and $H_{ij}$ satisfy the commutation relations of $X, Y, H$ in $\mathfrak{sl}(2,\mathbf{C})$ , which is true because the extra column/row of zeros doesn't affect the calculation.

3.30 This gives us three $\mathfrak{sl}(2,\mathbf{C})$ -subalgebras in $\mathfrak{sl}(3,\mathbf{C})$ . Because of this, any $\mathfrak{sl}(3,\mathbf{C})$ representation $V$ splits as an $\mathfrak{sl}(2,\mathbf{C})$ -representation in three ways.

Example:

4.00 I'll explain how this works in the example of the adjoint representation. With respect to the subalgebra spanned by $E_{13},E_{31},H_{13}$ , we see that the weight spaces of the adjoint representation of $\mathfrak{sl}(3,\mathbf{C})$ fall into three subsets which lie along lines parallel to $L_{1}-L_{3}$ :

5.15 the points $L_{2}-L_{1}$ and $L_{2}-L_{3}$ at the top left of the figure;
the points $L_{1}-L_{2}$ and $L_{3}-L_{2}$ at the bottom right of the figure;
the points $L_{1}-L_{3}$ , $0$ and $L_{3}-L_{1}$ across the middle.

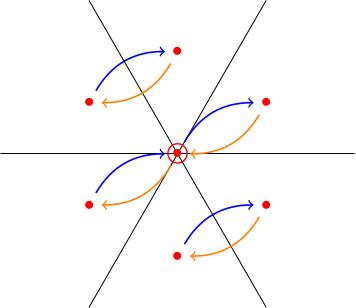
The adjoint representation decomposing as a direct sum of representations of an sl(2,C) subalgebra

Because the arrows show the action of the $\mathfrak{sl}(2,\mathbf{C})$ -subalgebra spanned by $E_{13},E_{31},H_{13}$ , we see that the direct sums of these weight spaces form subrepresentations $W_{L_{2}-L_{1}}\oplus W_{L_{2}-L_{3}},\quad W_{L_{1}-L_{2}}\oplus W_{L_{3}-L_{% 2}},\quad W_{L_{1}-L_{3}}\oplus W_{0}\oplus W_{L_{3}-L_{1}}.$ Moreover, we can read off the weights of the $\mathfrak{sl}(2,\mathbf{C})$ -subalgebra:

$W_{L_{2}-L_{1}}\oplus W_{L_{2}-L_{3}}$ has the weight diagram of the standard representation,
$W_{L_{1}-L_{2}}\oplus W_{L_{3}-L_{2}}$ also has the weight diagram of the standard representation,
$W_{L_{1}-L_{3}}\oplus W_{0}\oplus W_{L_{3}-L_{1}}$ has the weight diagram of $\mathrm{Sym}^{2}(\mathbf{C}^{2})\oplus\mathbf{C}$ because $W_{0}$ is 2-dimensional.

Example:

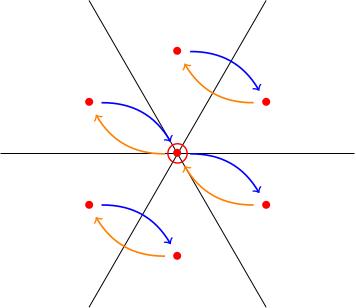
We would get a similar picture for the action of the subalgebra spanned by $E_{12},E_{21},H_{12}$ :

The adjoint representation decomposing as a direct sum of representations of another sl(2,C) subalgebra

Weyl symmetry

6.30 Recall that $\mathfrak{sl}(2,\mathbf{C})$ weight diagrams are symmetric about the origin. This means that for each of our three $\mathfrak{sl}(2,\mathbf{C})$ -subalgebras, our weight diagram has a reflection symmetry in the line orthogonal to the corresponding root.

Corollary:

The weight diagram of any $SU(3)$ -representation has three lines of reflection symmetry as shown in the figure below.

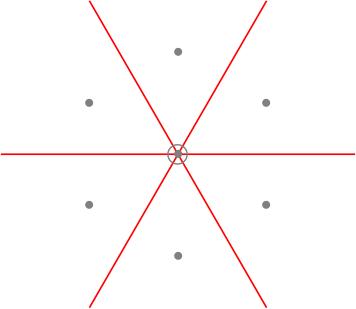
The three lines of reflection for the Weyl group of SU(3), superimposed on the root diagram

Remark:

8.00 This reflection symmetry is an honest Euclidean symmetry because we have drawn our weight diagram on a triangular lattice. We will discuss this more when we talk about the Killing form.

Definition:

The group of symmetries generated by these three reflection is called the Weyl group.

Example:

8.45 Consider the standard representation $\mathbf{C}^{3}$ . We saw that the weight diagram is the equilateral triangle with vertices at $L_{1},L_{2},L_{3}$ . The three lines of reflective Weyl symmetry are precisely the lines of symmetry of this equilateral triangle.

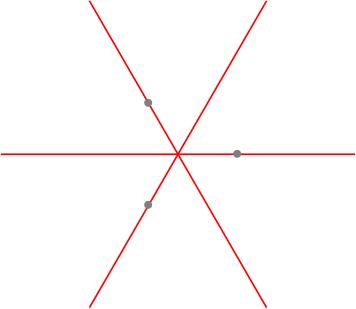
The Weyl symmetry group is precisely the symmetry group of the triangular weight diagram of the standard representation

We can see from this that the Weyl group is isomorphic to the symmetry group of an equilateral triangle. It has size 6 (three reflections, three rotations including the identity). If $\lambda$ is a weight which occurs in the weight decomposition of a representation then $\sigma(\lambda)$ also occurs for any $\sigma$ in the Weyl group. Thus each weight occurs in an orbit of the Weyl group: by the orbit-stabiliser theorem, this will have size 6 (if the weight doesn't lie on any of the lines of reflection) or size 3 (if the weight is stabilised by one of the reflections) which is why our weight diagrams will be hexagons and triangles.

Pre-class exercise

Exercise:

How does $\mathrm{Sym}^{3}(\mathbf{C}^{3})$ decompose into irreps of the $\mathfrak{sl}(2,\mathbf{C})$ -subalgebra spanned by $E_{12}$ , $E_{21}$ and $H_{12}$ ?