Classification of irreducible SU(3) representations

Statement

0.00 The point of this video is to give a recipe for constructing the weight diagrams of irreducible representations of $SU(3)$ .

Theorem:

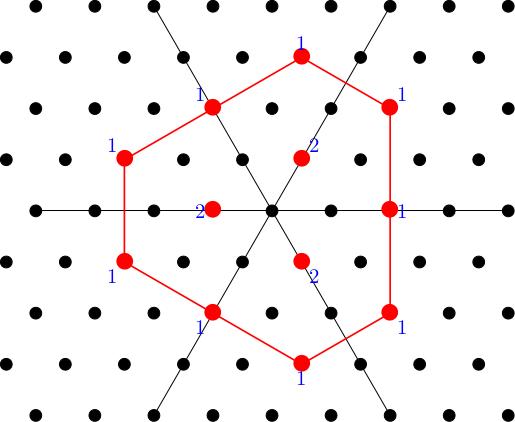
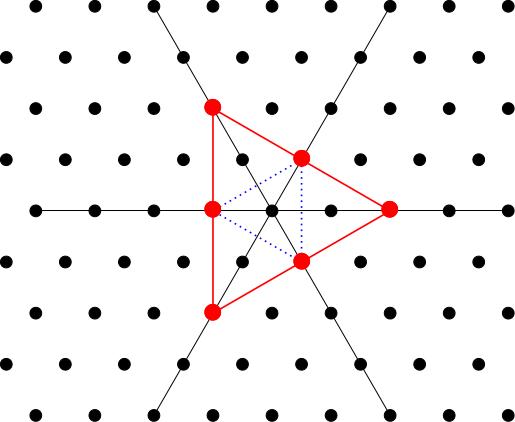
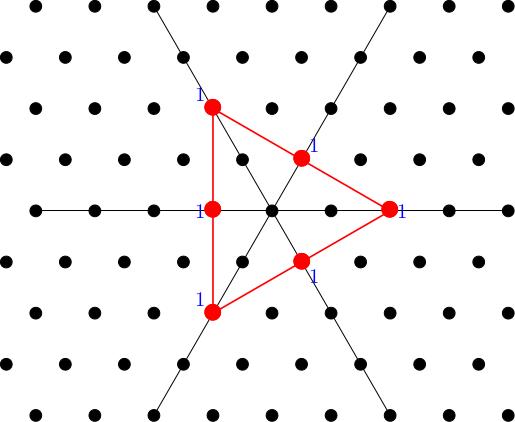
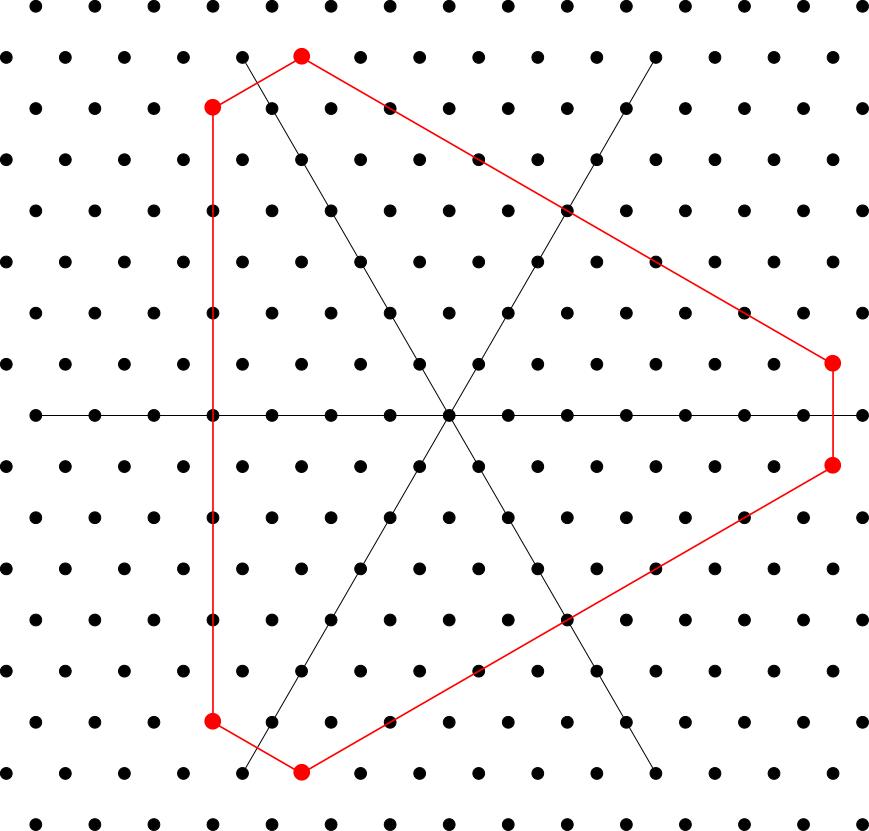
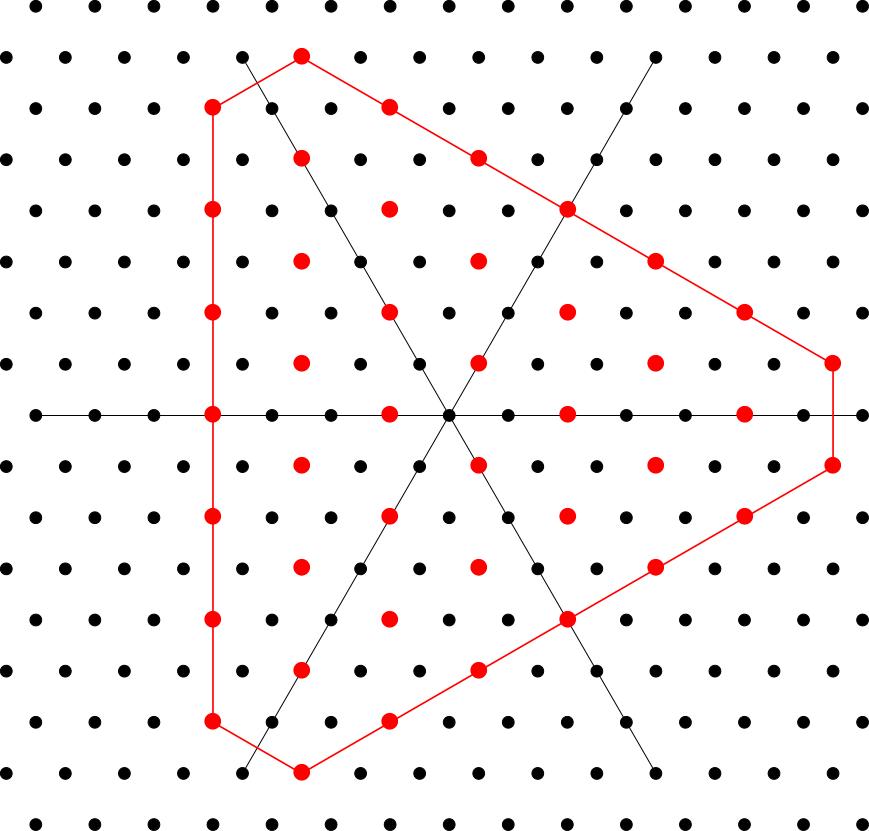
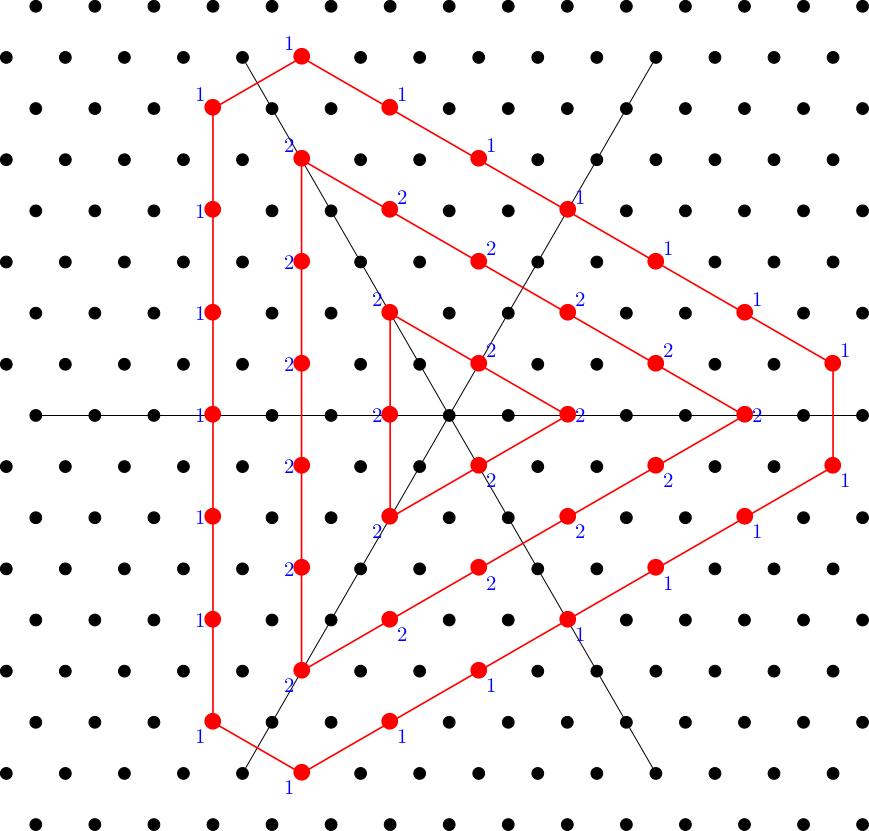
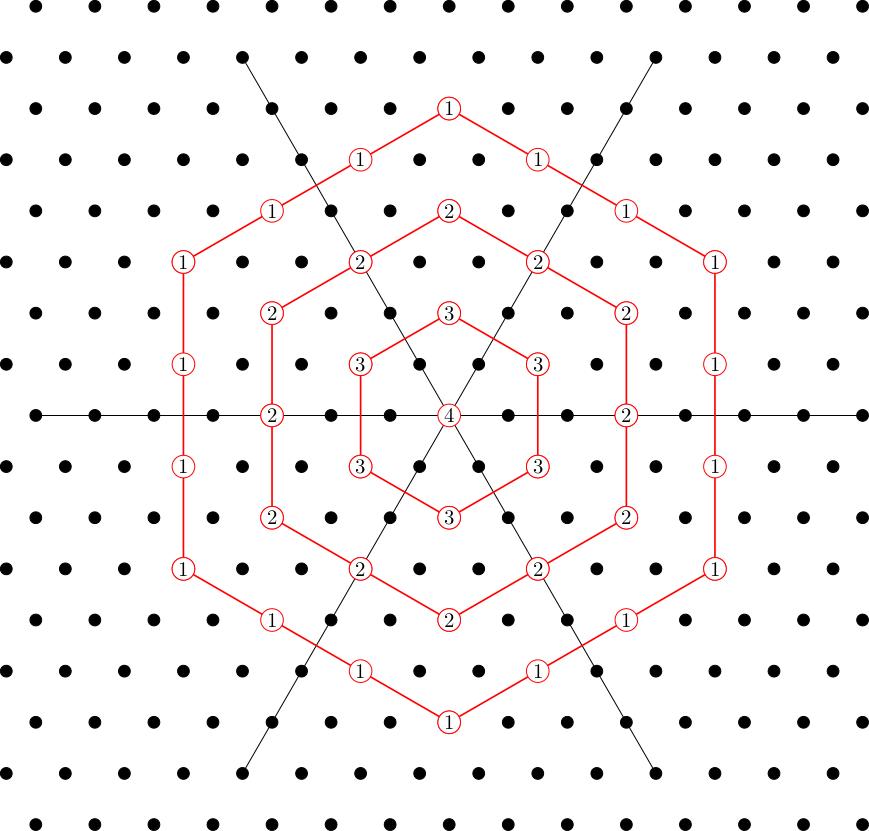
For any pair of nonnegative integers $k$ and $\ell$ there exists an irreducible representation of $SU(3)$ whose weight diagram is given by the following recipe. Moreover, any other irrep with the same weight diagram is isomorphic to $\Gamma_{k\ell}$ , and every irrep has its weight diagram constructed in this way. (We'll illustrate the recipe in the case $k=1$ , $\ell=2$ ):

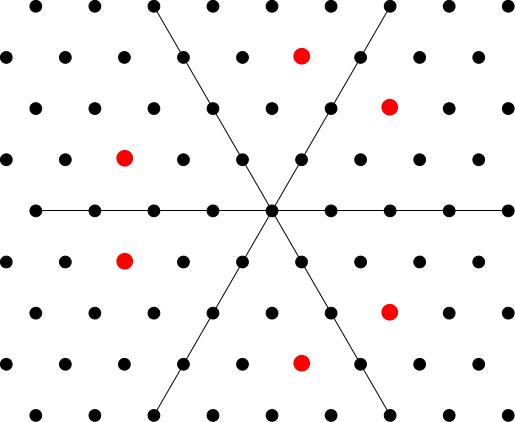
0.50 Take $\lambda=kL_{1}-\ell L_{3}$ and apply the six elements of the Weyl group to get six (or possibly three) points in the weight lattice.
3.15 Join these dots to get a convex polygon $P$ (more formally, we say that you take the convex hull of these points).
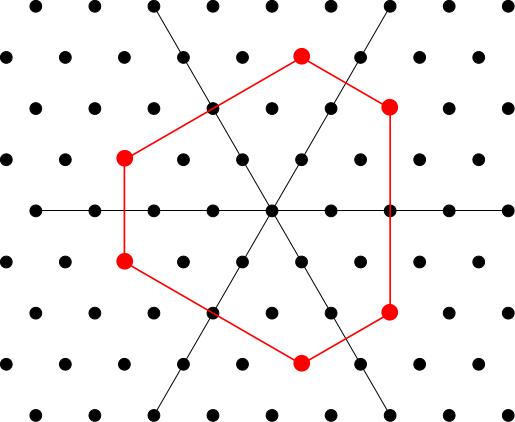
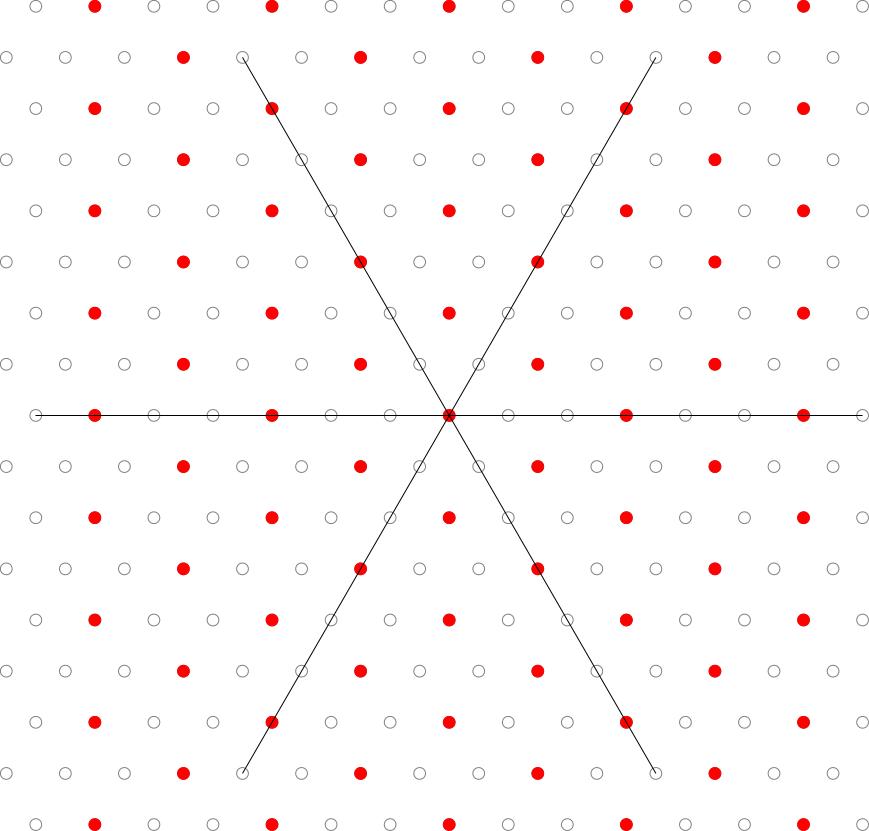
4.40 The weight diagram will consist of lattice points (i.e. integer linear combinations of $L_{1},L_{2},L_{3}$ ) contained in the polygon $P$ . We don't get all of the lattice points in $P$ , just as for $SU(2)$ we didn't get all integer points in some interval. Take all the points inside $P$ of the form $\lambda+r$ where $r$ is in the root lattice, that is the lattice of integer linear combinations of roots $L_{i}-L_{j}$ . Here is a picture of the root lattice:

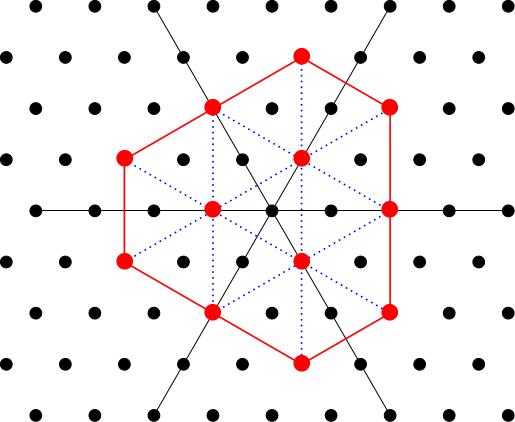
7.33 and here are the lattice points appearing in the weight diagram for our example $k=1$ , $\ell=2$ . I have also added some blue lines which point along the root directions just to help you see why this is the right answer in this case.
8.00 For each weight in the diagram, we need to describe the weight space. It's enough to say what its dimension is; this is usually called the multiplicity of the weight space. For $SU(2)$ , all weight spaces for an irreducible representation were 1-dimensional, but that's no longer true for $SU(3)$ . Instead, we follow the prescription described in the section below.

Remark:

9.08 The final point here is quite subtle. Even for $SU(3)$ , I won't justify the results below. In general, we should use one of the many formulae in the literature to determine the multiplicities of weight spaces. For example, there's a formula called the Freudenthal multiplicity formula which gives you the answer directly, and a beautiful formula called Weyl's character formula which tells you all the multiplicities packaged together in something like a generating function.

Multiplicities

9.30 For any weight on the boundary of $P$ , the multiplicity is 1 (for an irrep). Now, we peel off the outer polygon and we're left with a smaller polygon inside. The weights on the boundary of this smaller polygon will all have the same multiplicity, and this is:

one bigger than the previous multiplicity if the thing we just peeled off was a hexagon,
the same as the previous multiplicity if the thing we just peeled off was a triangle.

Now we peel off this polygon and repeat until we have exhausted our weight diagram.

Example:

This algorithm applied to our example $k=1$ , $\ell=2$ yields the following: weights on the outer hexagon have multiplicity 1, weights on the inner triangle have multiplicity 2.

More examples

Example:

10.55 Let's start with $\lambda=2L_{1}$ , that is $k=2$ , $\ell=0$ . Applying the Weyl group, we now get three vertices $2L_{1},2L_{2},2L_{3}$ (i.e. a triangular weight diagram). The polygon $P$ looks like this:

Starting at $\lambda$ , we move in all the possible root directions and add in those lattice points we reach provided they are contained in $P$ . This gives the following lattice points:

The lattice points in the weight diagram for k = 2, l = 0

The multiplicities on the outer triangle are all 1, and there is nothing left when we peel it off, so this is everything.

Remark:

This is the weight diagram of $\mathrm{Sym}^{2}(\mathbf{C}^{3})$ that we saw in an earlier video.

Example:

12.38 Take $k=6$ , $\ell=1$ , that is $\lambda=6L_{1}+L_{2}$ . Taking the convex hull of the images of $\lambda$ under the Weyl group gives the polygon below:

The convex hull of the weight diagram when k = 6, l = 1

13.53 The lattice points we get are shown below.

The lattice points of the weight diagram when k = 6, l = 1

14.00 The multiplicities are all 1 on the outermost hexagon. When we strip off this hexagon, we're left with a triangle. These all get multiplicity 2. When we strip off this triangle, we're left with another triangle and these all get multiplicity 2 (because we stripped off a triangle). When we strip off this final triangle, we're left with nothing, so that's it.

Example:

15.20 If $k=3$ and $\ell=3$ then we get the following answer.

The weight diagram when k = 3 and l = 3: three concentric hexagons and the origin, the multiplicities being 1, 2, 3, 4

In the next video we will use this to decompose some tensor products of $SU(3)$ representations, then we will come back and prove everything except the multiplicity formula.

Pre-class exercise

Exercise:

Find the weight diagrams of $\Gamma_{3,0}$ and $\Gamma_{3,1}$ .