Decomposing SU(3) representations

Example

Let's decompose V equals C 3 tensor C 3 tensor C 3 into irreducible representations of SU(3). We first need to find the weight diagram of V. Recall that C 3 has basis vectors e_1, e_2, e_3 with weights L_1, L_2, L_3.

A basis of V is therefore given by the vectors e_i tensor e_j tensor e_k.

Lemma:

e_i tensor e_j tensor e_k is a weight vector with weight L_i + L_j + L_k.

Proof:

If we act using H_theta, the diagonal matrix with diagonal entries theta_1, theta_2, theta_3 then we get H_theta applied to e_i tensor e_j tensor e_k equals (H_theta e_i) tensor e_j tensor e_k, plus e_i tensor (H_theta e_j) tensor e_k, plus e_i tensor e_j tensor (H_theta e_k) using the Leibniz rule (because H_theta is an element of the Lie algebra and this is how Lie algebras act on tensor products). Therefore, since H_theta e_i equals theta_i e_i, we get: H_theta applied to e_i tensor e_j tensor e_k equals (theta_i + theta_j + theta_k) times e_i tensor e_j tensor e_j, which equals (L_i + L_j + L_k) of theta times e_i tensor e_j tensor e_k.

Therefore e_1 tensor e_1 tensor e_1 is in W_{3 L_1} etc. We now plot all the points L_i + L_j + L_k in our weight diagram. Some of these points, like 2 L_1 + L_2, come from several weight vectors, like e_1 tensor e_1 tensor e_2, e_1 tensor e_2 tensor e_1, e_2 tensor e_1 tensor e_1. We keep track of this by writing the dimension of the weight space in the diagram. The sum of all dimensions should be 27, the total number of basis vectors.

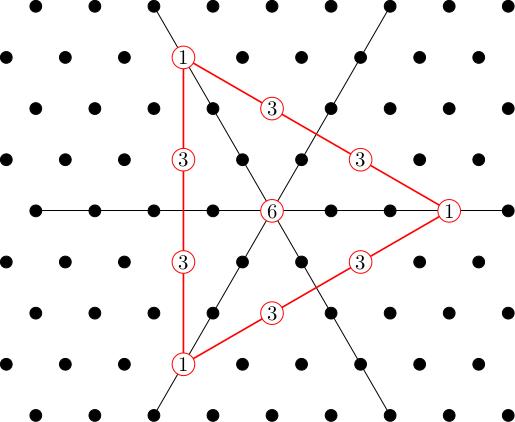
The weight diagram of C 3 tensor cubed

This is not the weight diagram of an irreducible representation; for example, the multiplicities around the outer triangle are not all equal to 1. We will decompose it into irreducible subrepresentations as we did for SU(2). We will do this by picking a "highest weight vector", generating an irreducible subrepresentation, taking its orthogonal complement with respect to an invariant Hermitian inner product (stripping off the corresponding weights from the diagram) and iterating this procedure.

There is no unique way to define "highest weight" any more, and we will discuss this point in a later video when we prove the classification theorem, but I claim that the highest weights will be vertices of our polygon. For example, we could take 3 L_1 in this example. This generates a subrepresentation whose weight diagram is:

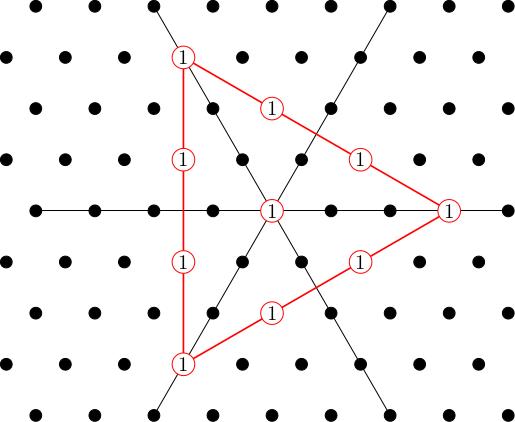
The weight diagram of Gamma_{3,0}

I'll call this Gamma_{3 0} (and more generally, Gamma_{m n} will denote the unique irrep with highest weight m L_1 minus n L_3).

The orthogonal complement to this subrepresentation has weight diagram:

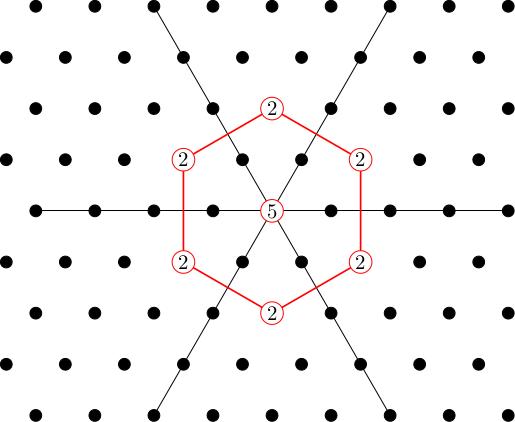
The weight diagram of the orthogonal complement of the subrepresentation isomorphic to Gamma_{3,0}

If we pick a highest weight vector in W_{L_1 + L_2} then we will generate a copy of Gamma_{1,1} inside our representation. We get two of these because W_{L_1 + L_2} is 2-dimensional. The weight diagram of Gamma_{1,1} is:

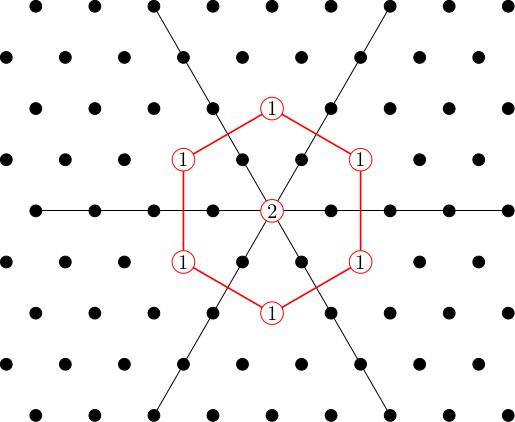
The weight diagram of Gamma_{1,1}

In other words, Gamma_{1,1} is isomorphic to the adjoint representation. What's left when I strip off these subrepresentations, I am left with a 1-dimensional W_0, which gives us a copy of the trivial 1-dimensional representation Gamma_{0,0} isomorphic to C.

Overall, we get C 3 tensor C 3 tensor C 3 splits as a direct sum of subrepresentations isomorphic to Gamma_{3,0}, Gamma_{1,1}, Gamma_{1,1} and C.

Pre-class exercise

Exercise:

Decompose C 3 tensor C 3 into irreducible subrepresentations.