Decomposing SU(3) representations

Example

0.00 Let's decompose $V=\mathbf{C}^{3}\otimes\mathbf{C}^{3}\otimes\mathbf{C}^{3}$ into irreducible representations of $SU(3)$ . We first need to find the weight diagram of $V$ . Recall that $\mathbf{C}^{3}$ has basis vectors $e_{1},e_{2},e_{3}$ with weights $L_{1},L_{2},L_{3}$ .

1.00 A basis of $V$ is therefore given by the vectors $e_{i}\otimes e_{j}\otimes e_{k}$ .

Lemma:

$e_{i}\otimes e_{j}\otimes e_{k}$ is a weight vector with weight $L_{i}+L_{j}+L_{k}$ .

Proof:

If we act using $H_{\theta}=\begin{pmatrix}\theta_{1}&0&0\\ 0&\theta_{2}&0\\ 0&0&\theta_{3}\end{pmatrix}$ then we get $H_{\theta}(e_{i}\otimes e_{j}\otimes e_{k})=(H_{\theta}e_{i})\otimes e_{j}% \otimes e_{j}+e_{i}\otimes(H_{\theta}e_{j})\otimes e_{k}+e_{i}\otimes e_{j}% \otimes(H_{\theta})e_{k}$ using the Leibniz rule (because $H_{\theta}$ is an element of the Lie algebra and this is how Lie algebras act on tensor products). Therefore, since $H_{\theta}e_{i}=\theta_{i}e_{i}$ , we get: $H_{\theta}(e_{i}\otimes e_{j}\otimes e_{k})=\theta_{i}+\theta_{j}+\theta_{k})e% _{i}\otimes e_{j}\otimes e_{k}=(L_{i}+L_{j}+L+k)(\theta)e_{i}\otimes e_{j}% \otimes e_{k}.$

2.35 Therefore $e_{1}\otimes e_{1}\otimes e_{1}\in W_{3L_{1}}$ etc. We now plot all the points $L_{i}+L_{j}+L_{k}$ in our weight diagram. Some of these points, like $2L_{1}+L_{2}$ , come from several weight vectors, like $e_{1}\otimes e_{1}\otimes e_{2}$ , $e_{1}\otimes e_{2}\otimes e_{1}$ , $e_{2}\otimes e_{1}\otimes e_{1}$ . We keep track of this by writing the dimension of the weight space in the diagram. The sum of all dimensions should be 27, the total number of basis vectors.

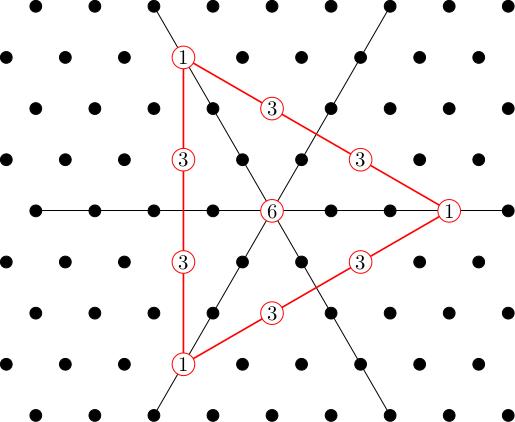
5.35 This is not the weight diagram of an irreducible representation; for example, the multiplicities around the outer triangle are not all equal to 1. We will decompose it into irreducible subrepresentations as we did for $SU(2)$ . We will do this by picking a "highest weight vector", generating an irreducible subrepresentation, taking its orthogonal complement with respect to an invariant Hermitian inner product (stripping off the corresponding weights from the diagram) and iterating this procedure.

6.05 There is no unique way to define "highest weight" any more, and we will discuss this point in a later video when we prove the classification theorem, but I claim that the highest weights will be vertices of our polygon. For example, we could take $3L_{1}$ in this example. This generates a subrepresentation whose weight diagram is:

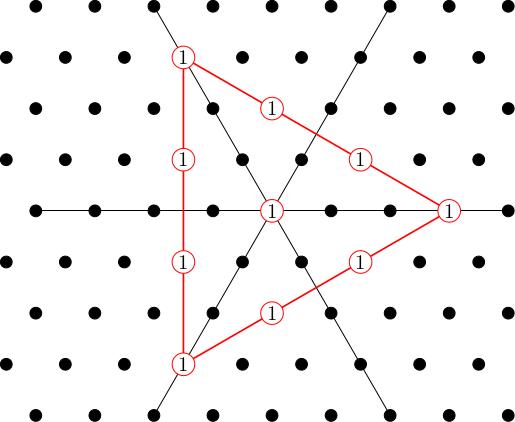
8.10 I'll call this $\Gamma_{3,0}$ (and more generally, $\Gamma_{m,n}$ will denote the unique irrep with highest weight $mL_{1}-nL_{3}$ ).

9.15 The orthogonal complement to this subrepresentation has weight diagram:

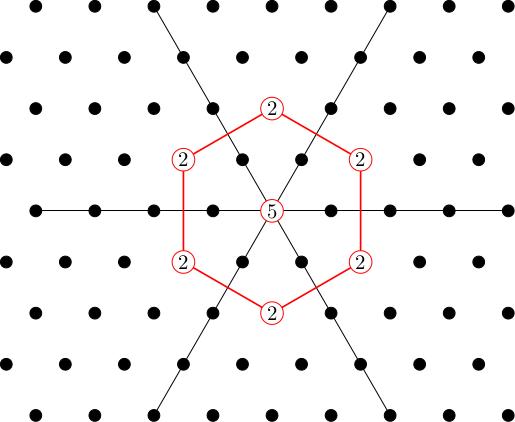
The weight diagram of the orthogonal complement of the subrepresentation isomorphic to Gamma_{3,0}

10.35 If we pick a highest weight vector in $W_{L_{1}+L_{2}}$ then we will generate a copy of $\Gamma_{1,1}$ inside our representation. We get two of these because $W_{L_{1}+L_{2}}$ is 2-dimensional. The weight diagram of $\Gamma_{1,1}$ is:

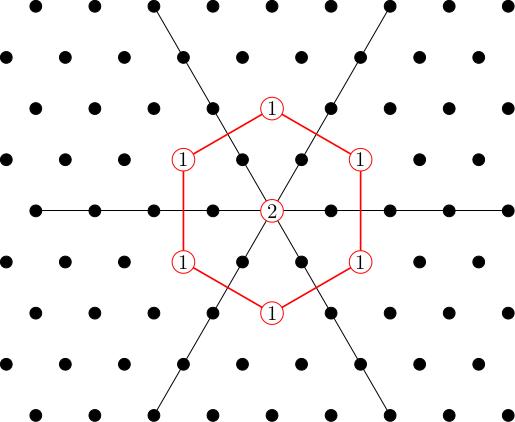
In other words, $\Gamma_{1,1}$ is isomorphic to the adjoint representation. What's left when I strip off these subrepresentations, I am left with a 1-dimensional $W_{0}$ , which gives us a copy of the trivial 1-dimensional representation $\Gamma_{0,0}\cong\mathbf{C}$ .

11.55 Overall, we get $\mathbf{C}^{3}\otimes\mathbf{C}^{3}\otimes\mathbf{C}^{3}\cong\Gamma_{3,0}% \oplus\Gamma_{1,1}\oplus\Gamma_{1,1}\oplus\mathbf{C}.$

Pre-class exercise

Exercise:

Decompose $\mathbf{C}^{3}\otimes\mathbf{C}^{3}$ into irreducible subrepresentations.