Classification of root systems, 1

Root systems

Recap

0.00 We have just introduced the notion of a root system, which is a finite set $R$ of vectors in $\mathbf{R}^{n}$ satisfying a bunch of axioms, which are supposed to encapsulate what it means to be the root diagram of a compact semisimple group.

The axioms are:

$\alpha\in R$ implies $-\alpha\in R$ .
$P_{\alpha}(\beta)=\frac{1}{2}n_{\beta\alpha}\alpha$ for some $n_{\beta\alpha}\in\mathbf{Z}$ , where $P_{\alpha}$ denotes orthogonal projection onto the line $\lambda_{\alpha}$ through $\alpha$ .
$R$ is symmetric under reflection in the hyperplane $\pi_{\alpha}$ orthogonal to the line $\lambda_{\alpha}$ (the root hyperplanes).
$\lambda_{\alpha}\cap R=\{-\alpha,\alpha\}$ .

Root systems are root diagrams

Theorem:

1.30 Every root system is the root diagram of a compact semisimple Lie group. The root diagram determines the Lie algebra of this group up to isomorphism.

Remark:

The root diagram doesn't determine the group up to isomorphism. For example, $SU(2)$ and $SO(3)$ have the same Lie algebra, and hence the same root diagram, but they are not isomorphic groups.

2.15 I'm not going to prove this theorem (not enough time left in the course), but you can do an in-depth project on it if you want. Instead, I will classify root systems up to isometry. Together with this theorem, this will yield a classification of Lie algebras of compact semisimple groups. In this video and the next, I will sketch the classification result. In the remaining videos, I will fill in some of the details.

Classification of root systems

2.55 Consider the root system of $SU(3)$ .

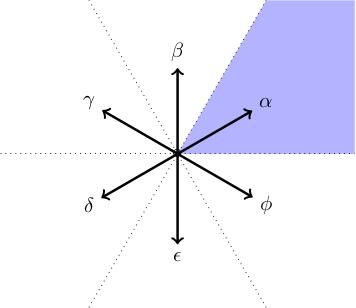
The root system of SU(3) with a roots alpha through phi sitting at angles 30, 90, 150,210, 270, 330, and a Weyl chamber subtending angles 0 through 60 degrees

To understand all six roots $\alpha,\beta,\gamma,\delta,\epsilon,\phi$ , we only need to understand the shaded region of the root diagram, which is a triangular wedge bounded by two root hyperplanes $\pi_{\beta}$ and $\pi_{\phi}$ , containing the root $\alpha$ . This is because the other five triangular regions are obtained from this one by reflecting using the Weyl group. This region is called a Weyl chamber.

4.25 This Weyl chamber is cut out by just two of the root hyperplanes (not all three). More precisely, I have picked a line of irrational slope (green in the figure below: a line through the origin which doesn't contain any other points in the weight lattice) which divides my roots into negative roots ( $\gamma,\delta,\epsilon$ on the left hand side) and positive roots ( $\phi,\alpha,\beta$ on the right hand side). This turns out to be enough to distinguish a subset of the roots called simple roots which cut out a specific Weyl chamber. We will see this in a later video. A different choice of line of irrational slope would give us a different set of simple roots.

Lemma:

6.30 The number of simple roots is $n$ , the dimension of the root system. Moreover, if $\beta$ and $\phi$ are simple roots then $\beta\cdot\phi<0$ .

We will prove this in a later video.

Example:

In the example above, there are two simple roots because the root system lives in the plane. Moreover, the dot product between them is negative ( $\beta$ points vertically up, $\phi$ points down and right).

7.40 I want to think of the boundary of the Weyl chamber as mirrors. The whole diagram would appear (via reflections and reflections of reflections etc) if you just put two mirrors at 60 degrees and looked into the chamber they make.

8.20 The photograph below shows what I'm talking about. It is a polyhedral kaleidoscope made of three mirrors. The reflections of the red Lego brick form the root diagram of $SU(4)$ . The pairs of mirrors make angles of $60$ degrees, $60$ degrees and $90$ degrees, which is what tells us we have the root system of $SU(4)$ . In the next video, we will continue the discussion by talking about the possible angles between mirrors in a root system.

Weyl chamber of the root system of SU(4), made using mirrors