Every root system is the root diagram of a compact semisimple Lie group. The root diagram determines the Lie algebra of this group up to isomorphism.
Classification of root systems, 1
Root systems
Recap
We have just introduced the notion of a root system, which is a finite set R of vectors in R n satisfying a bunch of axioms, which are supposed to encapsulate what it means to be the root diagram of a compact semisimple group.
The axioms are:
-
alpha is in R implies minus alpha is in R.
-
P_alpha of beta equals a half n beta alpha times alpha for some integer n beta alpha, where P_alpha denotes orthogonal projection onto the line lambda_alpha through alpha.
-
R is symmetric under reflection in the hyperplane \pi_\alpha orthogonal to the line lambda alpha (the
root hyperplanes ). -
lambda alpha intersect R equals the set minus alpha, alpha.
Root systems are root diagrams
The root diagram doesn't determine the group up to isomorphism. For example, SU(2) and SO(3) have the same Lie algebra, and hence the same root diagram, but they are not isomorphic groups.
I'm not going to prove this theorem (not enough time left in the course), but you can do an in-depth project on it if you want. Instead, I will classify root systems up to isometry. Together with this theorem, this will yield a classification of Lie algebras of compact semisimple groups. In this video and the next, I will sketch the classification result. In the remaining videos, I will fill in some of the details.
Classification of root systems
Consider the root system of SU(3).
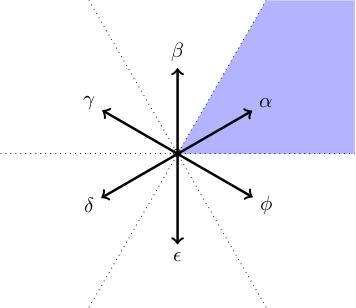
To understand all six roots alpha, beta, gamma, delta, epsilon, phi, we only need to understand the shaded region of the root diagram, which is a triangular wedge bounded by two root hyperplanes pi_beta and pi_phi, containing the root alpha. This is because the other five triangular regions are obtained from this one by reflecting using the Weyl group. This region is called a
This Weyl chamber is cut out by just two of the root hyperplanes (not all three). More precisely, I have picked a line of irrational slope (green in the figure below: a line through the origin which doesn't contain any other points in the weight lattice) which divides my roots into negative roots (gamma, delta, epsilon on the left hand side) and positive roots (phi, alpha, beta on the right hand side). This turns out to be enough to distinguish a subset of the roots called
The number of simple roots is n, the dimension of the root system. Moreover, if beta and phi are simple roots then beta dot phi is negative.
We will prove this in a later video.
In the example above, there are two simple roots because the root system lives in the plane. Moreover, the dot product between them is negative (beta points vertically up, phi points down and right).
I want to think of the boundary of the Weyl chamber as mirrors. The whole diagram would appear (via reflections and reflections of reflections etc) if you just put two mirrors at 60 degrees and looked into the chamber they make.
The photograph below shows what I'm talking about. It is a polyhedral kaleidoscope made of three mirrors. The reflections of the red Lego brick form the root diagram of SU(4). The pairs of mirrors make angles of 60 degrees, 60 degrees and 90 degrees, which is what tells us we have the root system of SU(4). In the next video, we will continue the discussion by talking about the possible angles between mirrors in a root system.
