Lie groups and Lie algebras: Questions 2

1. Derivative of A(t)^-1

(Depends only on material from Week 1.)

Let $A(t)$ be a family of matrices depending smoothly on a parameter $t$ .

1. Is it true or false that $\frac{d}{dt}(A{(t)}^n)=nA{(t)}^{n-1}\frac{dA}{dt}$ for all positive $n$ ? Give a proof or a counterexample.

2. Suppose that $A(t)$ is invertible for all $t$ . By differentiating the condition $A(t)A{(t)}^{-1}=I$ , find a formula for $\frac{d}{dt}\left(A{(t)}^{-1}\right)$

2. More about tangent spaces

(Depends on the video about the Lie algebra as the tangent space).

Suppose that $\gamma :𝐑\to G$ is a path in a matrix group $G$ .

1. Fix $s\in 𝐑$ and consider the path $\delta (t):=\gamma {(s)}^{-1}\gamma (s+t)$ . Find $\delta (0)$ and $\dot{\delta }(0)$ .

2. Hence or otherwise, show that $\gamma {(s)}^{-1}\frac{d\gamma (s)}{ds}$ is an element of the Lie algebra $𝔤$ .

3. The tangent space to $G$ at some point $g\in G$ is defined to be the set of all tangent vectors to paths $\gamma (t)\in G$ such that $\gamma (0)=g$ . Deduce from the previous part of the question that the tangent space to $G$ at $g$ equals $g𝔤$ .

3. Topological closure

(Depends on the video about matrix groups.)

Show that the topological closure of a subgroup $G\subset GL(n,𝐑)$ is a subgroup of $GL(n,𝐑)$ . [Hint: You may use the fact that the topological closure of $G$ is the set of all matrices in $GL(n,𝐑)$ arising as limits of sequences of matrices $M_k\in G$ .]

4. Heisenberg group

(Depends on the Lie algebra of a matrix group and the notion of commutator.)

The Heisenberg group $H_3$ is the group of 3-by-3 matrices of the form

1. What is its Lie algebra?

2. Verify that the exponential map is bijective for this group.

3. Find a basis for the Lie algebra such that each basis element has at most one nonvanishing matrix entry, and compute the commutators between your chosen basis elements.

5. Alternative proof that little g is a Lie algebra

(Depends on the videos about $𝔤$ as a tangent space and as a Lie algebra.)

Let $G$ be a matrix group with Lie algebra $𝔤$ . We will figure out an alternative proof that $𝔤$ is preserved by Lie bracket.

Suppose that $X,Y\in 𝔤$ . Let $Z:=\exp (sX)Y\exp (-sX)$ . By considering $\exp (tZ)$ , show that $Z\in 𝔤$ for all $s\in 𝐑$ . Why does this imply $[X,Y]\in 𝔤$ ?

(Hint: If $\gamma (s)$ is a path in a vector space then its tangent vector also belongs to this vector space. You may assume that $𝔤$ is a vector space.)

6. A subrepresentation

(Builds on the video about complete reducibility).

Recall that a representation is a homomorphism $R:G\to GL(n,𝐑)$ , and a subrepresentation is a subspace $V\subset {𝐑}^n$ such $v\in V$ implies $R(g)v\in V$ for all $g\in G$ .

Let $G$ be the group of real numbers with addition. Consider the homomorphism $R:G\to GL(2,𝐑)$ , . Show that the $x$ -axis is a subrepresentation (i.e. that $R(t)$ preserves the $x$ -axis for all $t\in 𝐑$ ). Are there any other subrepresentations? (Either exhibit one explicitly or prove there are none). Is $R$ completely reducible?

7. Symplectic group

(Depends on the idea of a matrix group and its Lie algebra).

Let $\mathrm{\Omega }$ be the $2n$ -by-$2n$ matrix given by $n$ -by-$n$ blocks Define $$Sp(2n,𝐑)=\{M\in GL(2n,𝐑):M^T\mathrm{\Omega }M=\mathrm{\Omega }\}.$$

1. Check that $Sp(2n,𝐑)$ is a group. Is it topologically closed?

2. Find the Lie algebra $𝔰𝔭(2n,𝐑)$ .

3. Show that $Sp(2n,𝐑)$ is an unbounded group (i.e. you can find a sequence of matrices $M_k\in Sp(2n,𝐑)$ such that some of the matrix entries of $M_k$ go to infinity as $k\to \mathrm{\infty }$ .

4. Show directly that if $X,Y\in 𝔰𝔭(2n,𝐑)$ then $[X,Y]\in 𝔰𝔭(2n,𝐑)$ . Is it true that $XY\in 𝔰𝔭(2n,𝐑)$ for all $X,Y\in 𝔰𝔭(2n,𝐑)$ ?

8. Lorentz group

(Builds on the example homomorphism $SU(2)\to SO(3)$ .)

Let $c\in 𝐑$ be a positive constant (the speed of light!). Define $\eta$ to be the $4$ -by-$4$ matrix and define $$O(1,3)=\{M\in GL(4,𝐑):M^T\eta M=\eta \}.$$ This is called the Lorentz group: it consists of transformations of 4-dimensional spacetime preserving the "spacetime interval" $-c^2{t}^2+x^2+y^2+z^2$ .

1. Let $\zeta$ be a real number. Calculate and show it lives in $O(1,3)$ . This is called an (inverse) Lorentz boost, and it's the simplest Lorentz transformation which mixes up space with time.

2. Let's encode vectors $v=(t,x,y,z)$ as 2-by-2 matrices . Calculate $det(S_v)$

3. Show that $S_v$ is Hermitian, that is $S_v^{†}=S_v$ . Moreover, show that any Hermitian matrix is of the form $S_v$ for some $v\in {𝐑}^4$ .

4. Given a matrix $A\in SL(2,𝐂)$ , check that $A{S}_v{A}^{†}$ is Hermitian (note that this implies $A{S}_v{A}^{†}=S_{v^{\prime }}$ for some $v^{\prime }$ by the previous part of the question).

5. Define $F:SL(2,𝐂)\to O(1,3)$ implicitly by $S_{F(A)v}=A{S}_v{A}^{†}$ . Show that this is a homomorphism.

In fact, this homomorphism is 2-to-1 onto the identity component of the Lorentz group, so $SL(2,𝐂)$ is basically the spin group associated to $O(1,3)$ .

9. Discontinuous homomorphism

(Depends on the video about smooth homomorphisms.)

In this course, we're focusing on smooth homomorphisms, but it's quite possible to have homomorphisms which are not smooth (even discontinuous). In this question, we'll "construct" one.

1. Explain the sentence "$𝐑$ is a vector space over $𝐐$ ". Give me an example of two elements of $𝐑$ which are linearly independent over $𝐐$ .

2. For the rest of the question, we will assume we have picked a basis $B$ for this vector space. Note that this vector space is so awful that nobody has ever written down (or will ever write down) a basis explicitly. Can you explain why specifying a basis would be such a difficult problem?

3. For each $b\in B$ , pick a real number ${\lambda }_b$ . Define $$F:𝐑\to 𝐑,F\left(\sum _{b\in B}{c}_{b}b\right)=\sum _{b\in B}{\lambda }_b{c}_{b}b,$$ (here, the notation means that ${\sum }_{b\in B}{c}_{b}b$ is the unique vector whose $b$ -component is $c_b$ ). If we equip $𝐑$ with addition, show that $F$ is a homomorphism.

4. Suppose not all the ${\lambda }_b$ are equal. Why is $F$ not smooth?

10. Neighbourhood of the identity generates

(Technically no prerequisites, but requires you to know the Heine-Borel theorem from analysis. This is a hint about how to solve the problem!)

Let $G$ be a matrix group and let $S\subset G$ be an open neighbourhood of the identity matrix.

1. By considering the set $S^{-1}:=\{s^{-1}:s\in S\}$ show that there is a smaller open neighbourhood $S_1$ of the identity such that $g\in S_1$ implies $g^{-1}\in S_1$ . Henceforth, we will drop the subscript $1$ and just assume that $S$ always had this property.

2. Let $\gamma :[0,1]\to G$ be a continuous path in $G$ with $\gamma (0)=I$ . Prove that $\gamma (1)=s_1{s}_2\mathrm{\cdots }{s}_N$ for some sequence of elements $s_i\in S$ . You may use the following diagram as inspiration for coming up with the proof, provided you explain what it's trying to depict and how it is constructed.

   

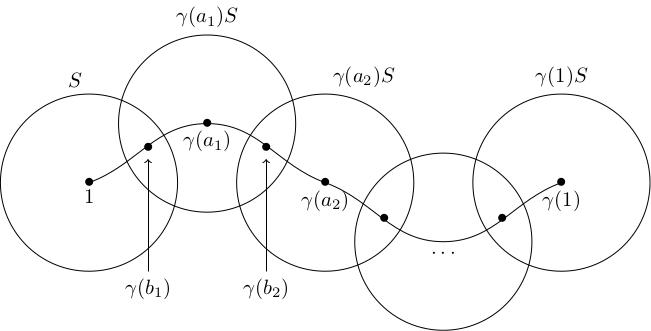
This tells us that any neighbourhood of the identity generates the path component of the identity in $G$ .

11. More about the Heisenberg group

(Depends on the earlier question about this group and the video about smooth homomorphisms.)

Consider the subgroup

1. Show that elements of $N_3$ commute with everything in $H_3$ .

2. Show that elements of $N_3$ can be written in the form $gh{g}^{-1}{h}^{-1}$ for some $g,h\in H_3$ .

3. Deduce that if $R:H_3\to GL(n,𝐂)$ is a homomorphism then $det(R(g))=1$ for all $g\in N_3$ .

We will use these results in a later exercise to construct a (Lie) group which is not a matrix group.

12. Fourier theory

(Depends on the video about smooth homomorphisms).

Let $V$ be the (infinite-dimensional) vector space of complex-valued $2\pi$ -periodic functions $$f(\theta )\text{ such that }f(\theta +2\pi )=f(\theta ).$$ We will define a homomorphism $R:U(1)\to GL(V)$ , where $GL(V)$ now denotes the space of invertible linear maps $V\to V$ . Define $R(e^{i\varphi })$ to be the linear map which takes a function $f(\theta )$ to $f(\theta +\varphi )$ .

1. Check that $R(e^{i\varphi })$ is linear.

2. Check that $R$ is a homomorphism.

3. Fix an integer $n$ . Suppose that $f$ is an eigenvector of $R(e^{i\varphi })$ with eigenvalue $e^{in\varphi }$ for all $\varphi$ . I claim this completely determines $f$ up to an overall constant factor: what is $f$ ?

We will later see that these are the only possible eigenvalues.