1.01 Winding numbers and the fundamental theorem of algebra

Below the video you will find accompanying notes and some pre-class questions.

• Next video: 1.02 Paths, loops and homotopies.
• Index of all lectures.

Notes

(0.00) I want to start this module by giving a rough sketch of how to prove the fundamental theorem of algebra using the idea of winding numbers. You may have seen something similar in a first course on complex analysis, where the winding number was defined using a contour integral. The aim of the current proof is to remove the need for complex analysis in this definition: the winding number is something purely topological.

The fundamental theorem of algebra

(1.45) Let $p\colon\mathbf{C}\to\mathbf{C}$, $p(z)=z^n+a_{n-1}z^{n-1}+\cdots+a_0$, be a complex polynomial. Assume that $p$ has no complex root, in other words that there is no point $x\in\mathbf{C}$ for which $p(x)=0$. We will show that $n=0$, in other words that $p$ has only a constant term.

(2.24) Consider the circle of radius $R$ in the complex plane. The points in this circle are precisely those of the form $Re^{i\theta}$. Let $\gamma_R$ be the image of this circle under the map $p\colon\mathbf{C}\to\mathbf{C}$. We can think of $\gamma_R$ as a loop in $\mathbf{C}$:

$$\gamma_R(\theta)=p(Re^{i\theta}).$$ Crucially, because $p(z)\neq 0$ for all $z\in\mathbf{C}$, the loop $\gamma_R$ is a loop in $\mathbf{C}\setminus\{0\}$.

Figure 1. In this figure, we see the circle of radius $R$ in the domain of $p$ and its image $\gamma_R$ in the image of $p$ ($\mathbf{C}\setminus\{0\}$). In this example, $p(z)=z^3-z/2$ and $R=2$ and we see that the winding number of $\gamma_R$ is 3.

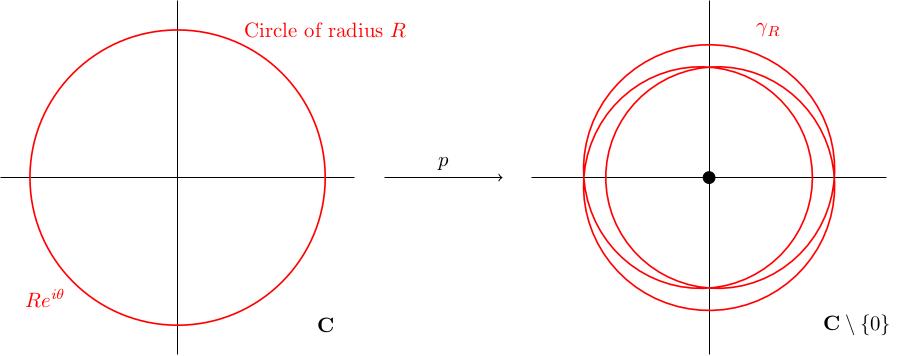
(3.54) When $R=0$, $\gamma_0(\theta)=p(0)$ is independent of $\theta$. In other words, $\gamma_0$ is the constant loop at the point $p(0)\in\mathbf{C}\setminus\{0\}$.

(4.42) When $R$ is very large, the term $z^n$ dominates in $p$, so $\gamma_R(\theta)\approx \delta(\theta)$, where $\delta(\theta)=R^ne^{in\theta}$.

Claim: (6.54) There is a homotopy invariant notion of winding number around the origin for paths in $\mathbf{C}\setminus\{0\}$ which gives zero for the constant loop and $n$ for the loop $\delta(\theta)=R^ne^{in\theta}$.

Homotopy invariant means, roughly, invariant under continuous deformations; in our situation, that means that the winding number of $\gamma_R$ around the origin should be independent of $R$. Since $\gamma_0$ has winding number zero and $\gamma_R$ has winding number $n$ for large $R$, this implies $n=0$.

Outlook

(9.24) The rest of this module will be about defining this notion of winding number, the notion of homotopy and homotopy invariance, and generalising it to other spaces. In a more general setting, the spaces we're interested in (in this example $\mathbf{C}\setminus\{0\}$) will have an associated group (in this example the integers $\mathbf{Z}$) called the fundamental group and loops will have winding ``numbers'' which are elements of this group.

This will have many applications, including:

• the Brouwer fixed point theorem (any continuous map from the 2-dimensional disc to itself has a fixed point).
• the fact that a trefoil knot cannot be unknotted.
• the fact that the three Borromean rings cannot be unlinked from one another (despite the fact that they can be unlinked in pairs ignoring the third).

Pre-class questions

1. Go through the rough sketch proof and highlight all the steps which seem to you not to be fully justified. We will discuss this in class, and I will call upon you for suggestions. Later in the module, we will revisit this proof and fill in all the gaps (hopefully to your satisfaction).

Navigation

• Next video: 1.02 Paths, loops and homotopies.
• Index of all lectures.