1.03 Concatenation and the fundamental group

Below the video you will find accompanying notes and some pre-class questions.

Previous video: 1.02 Paths, loops, and homotopies.
Next video: 1.04 Examples and simply-connectedness.
Index of all lectures.

Notes

Concatenation

(0.10) Let

$X$ be a topological space and suppose

$\alpha,\beta\colon[0,1]\to X$ are paths such that

$\alpha(1)=\beta(0)$ . The concatenation

$\beta\cdot\alpha$ is the path

$(\beta\cdot\alpha)(t)=\begin{cases}\alpha(2t)&\mbox{ if }t\in[0,1/2]\\\beta(2t-1)&\mbox{ if }t\in[1/2,1].\end{cases}$

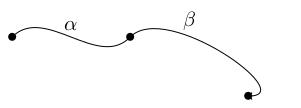
The fundamental group

(3.49) Given a topological space

$X$ and a basepoint

$x\in X$ , write

$\Omega_xX$ for the set of all loops in

$X$ based at

$x$ . The relation

$\simeq$ that two loops

$\alpha,\beta\in\Omega_xX$ are based-homotopic is an equivalence relation. We write

$\pi_1(X,x)$ for the set of equivalence classes

$\Omega_xX/\simeq$ of loops up to based homotopy.

We can make

$\pi_1(X,x)$ into a group under concatenation: if

$[\alpha]\in\pi_1(X,x)$ denotes the homotopy class of the loop

$\alpha$ then \\alpha.\]

The operation

$[\beta]\cdot[\alpha]=[\beta\cdot\alpha]$ defines a group structure on

$\pi_1(X,x)$ . In particular:

it is well-defined on homotopy classes,
it is associative,
it has an identity (the identity element is the constant loop $\epsilon(t)=x$ ),
each homotopy class of loops $[\gamma]$ has an inverse $[\bar{\gamma}]$ , where $\bar{\gamma}(t)=\gamma(1-t)$ is the loop which runs around $\gamma$ in reverse.

(8.30) We will show that the constant loop

$\epsilon$ is an identity for concatenation on

$\pi_1(X,x)$ ; the other parts are left as exercises.

The concatenation $\gamma\cdot\epsilon$ stays at $x$ for time $1/2$ and then moves around $\gamma$ at double-speed. This is not /equal to/ the loop $\gamma$ , but it only differs in the way it is parametrised. By playing with the parametrisation, we can construct a homotopy $\gamma_s$ from this concatenation to the original loop $\gamma$ .

$\gamma_s(t)=\begin{cases} \epsilon(t)&\mbox{ if }t\leq 1/2(1-s)\\ \gamma((2-s)t+s-1)&\mbox{ if }t\geq 1/2(1-s) \end{cases}$ (10.46) To understand this formula, observe that at the stage

$s$ in the homotopy, the loop

$\gamma_s$ stays at

$x$ for time

$1/2(1-s)$ (

$1/2$ when

$s=0$ and

$0$ when

$s=1$ ) then moves around

$\gamma$ at

$(2-s)$ times the speed of the original loop (twice as fast when

$s=0$ , the same speed as the original when

$s=1$ ). Here is a picture of the domain of the homotopy:

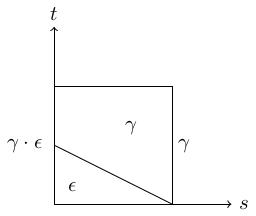
(14.46) This homotopy is continuous by one of the exercises we will do in class when we learn about topological spaces; it is a homotopy rel endpoints since $\gamma_s(0)=\gamma_s(1)=x$ for all $s$ ; and it satisfies $\gamma_0=\gamma\cdot\epsilon$ and $\gamma_1=\gamma$ . A similar homotopy works for $\epsilon\cdot\gamma$ .

Pre-class questions

Suppose that $\alpha_t$ is a homotopy between $\alpha_0$ and $\alpha_1$ and $\beta_t$ is a homotopy between $\beta_0$ and $\beta_1$ . Can you write down a homotopy between $\beta_0\cdot\alpha_0$ and $\beta_1\cdot\alpha_1$ ? This verifies one of the claims from the lemma in the video/notes: which claim?

Navigation

Previous video: 1.02 Paths, loops, and homotopies.
Next video: 1.04 Examples and simply-connectedness.
Index of all lectures.