Optional: Local exponential charts

2.05 We could like the same to work for any matrix group

$G\subset GL(n,\mathbf{R})$ . Namely, we would like to show:

Theorem:

If $G$ is a matrix group and $\mathfrak{g}$ is its Lie algebra then there are neighbourhoods $U^{\prime}\subset\mathfrak{g}$ of the zero matrix and $V^{\prime}\subset G$ of the identity such that $\exp(U^{\prime})=V^{\prime}$ and $\exp|_{U^{\prime}}\colon U^{\prime}\to V^{\prime}$ is invertible.

Proof:

3.00 Let $U^{\prime}=U\cap\mathfrak{g}$ and $V^{\prime}=V\cap G$ . First, we note that $\exp$ does indeed go from $\mathfrak{g}$ to $G$ by definition of $\mathfrak{g}$ , and $\exp(U)=V$ , so $\exp(U^{\prime})\subset V^{\prime}$ .

4.30 So what is left to prove? The map $\exp\colon U\to V$ is invertible, hence injective, so its restriction $\exp|_{U^{\prime}}$ must also be injective. But is $\exp|_{U^{\prime}}$ surjective? In other words, is it clear that $\log(V^{\prime})\subset U^{\prime}$ ?

5.40 This figure shows what you might imagine going wrong (we will later show that this doesn't happen, at least if you shrink $U$ and $V$ ). It shows a cartoon of a subgroup $G\subset GL(n,\mathbf{R})$ which "wraps back on itself" and gets very close to the identity but never quite gets there. You can now imagine that when you intersect with a very small $V$ (in red), $\exp(U^{\prime})$ (in blue) could end up missing this appendage of $G$ which wraps back towards the identity (in green), because to get to this appendage you have to exponentiate something very large. In other words, $\exp(U^{\prime})$ is the blue bit and $V^{\prime}$ is everything which is blue or green. In the end, we will show this doesn't happen, so this is a cartoon picture of something which doesn't happen. You therefore shouldn't be too annoyed if the picture doesn't make sense.

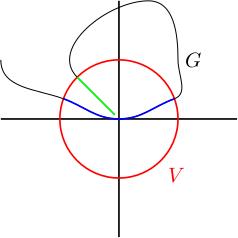
A fictitious subgroup G which wraps back on itself and comes close to the identity. This shows how it might be that exp(U') is smaller than V'.

7.55 If surjectivity of $\exp|_{U^{\prime}}$ fails then there's an element $g\in V^{\prime}=G\cap V$ such that $g\not\in\exp(U^{\prime})$ . We could try to fix this by shrinking $U$ and $V$ , but let's suppose that doesn't help us. This will mean there is a sequence $g_{i}\in V^{\prime}$ such that $g_{i}\to I$ and $g_{i}\not\in\exp(U^{\prime})$ for all $i$ (you should imagine a sequence of matrices on the green appendage, tending to the origin in the picture).

9.30 Let's assume that there is such a sequence and aim to derive a contradiction.

Recall that $\mathfrak{g}\subset\mathfrak{gl}(n,\mathbf{R})$ is a subspace. Pick a vector space complement $W$ for $\mathfrak{g}$ , that is $\mathfrak{g}\cap W=\{0\}$ and $\mathfrak{g}+W=\mathfrak{gl}(n,\mathbf{R})$ . 11.30 In the figure, $\mathfrak{g}$ is supposed to be the horizontal axis (tangent to $G$ at the identity) and $W$ is supposed to be the vertical axis.

12.10 I claim that the map $F\colon\mathfrak{g}\oplus W\to GL(n,\mathbf{R})$ defined by $F(v,w)=\exp(v)\exp(w)$ is locally invertible like $\exp$ , i.e. there exists a neighbourhood $N_{1}$ of $0\in\mathfrak{g}\oplus W$ and a neighbourhood $N_{2}$ of $I\in GL(n,\mathbf{R})$ such that $F(N_{1})=N_{2}$ and $F\colon N_{1}\to N_{2}$ is invertible. This is proved using the inverse function theorem, just like for $\exp$ (compute the derivative of $F$ at the zero map and show this derivative is invertible). I leave it as an exercise to fill in the details.

14.35 Therefore, if $g_{i}$ is sufficiently close to the identity (which it is for large $i$ ), then $g_{i}=\exp(v_{i})\exp(w_{i})$ for some sequence $v_{i}\in\mathfrak{g}$ and $w_{i}\in W$ .
15.20 Our sequence $g_{i}$ is not in $\exp(U^{\prime})$ , so $w_{i}\neq 0$ for all $i$ . In particular, we can divide $w_{i}$ by its matrix norm to get a matrix $w_{i}/\lVert w_{i}\rVert\in W$ with norm 1. Since the set of matrices with norm 1 is closed and bounded (compact), the sequence $w_{i}/\lVert w_{i}\rVert\in W$ converges to some matrix $w\in W$ with norm 1 (in particular, $w\neq 0$ ).
17.55 We are going to prove that $w\in\mathfrak{g}$ ; this will give us a contradiction, as $w\in W$ and $W$ is a complement for $\mathfrak{g}$ . For this, we need to show that $\exp(tw)\in G$ for all $t\in\mathbf{R}$ .

19.00 Fix $t$ . Consider $t/\lVert w_{i}\rVert$ and take its integer and fractional parts $t/\lVert w_{i}\rVert=n_{i}+\epsilon_{i}$ , $n_{i}\in\mathbb{N}$ , $\epsilon\in[0,1)$ . Since $g_{i}\to I$ as $i\to\infty$ , we know that $w_{i}\to 0$ , so $\lVert w_{i}\rVert\to 0$ , hence $t/\lVert w_{i}\rVert\to\infty$ (as $t$ is fixed) and hence $n_{i}\to\infty$ .
21.00 We want to show that $\exp(tw)\in G$ . First note that $\exp(w_{i})\in G$ for all $i$ because $\exp(w_{i})=\exp(-v_{i})g_{i}$ and $\exp(-v_{i})$ and $g_{i}$ are both in $G$ . Because $G$ is a group, $(\exp(w_{i}))^{n_{i}}\in G$ and $(\exp(w_{i}))^{n_{i}}=\exp(n_{i}w_{i})$ because $w_{i}$ commutes with itself. The sequence $\exp(n_{i}w_{i})=\exp(tw_{i}/\lVert w_{i}\rVert-\epsilon_{i}w_{i})$ converges to $\exp(tw)$ because $w_{i}/\lVert w_{i}\rVert\to w$ and $\epsilon_{i}w_{i}\to 0$ .

24.00 Because $G$ is topologically closed, this limit lives in $G$ , so $\exp(tw)\in G$ . This argument works for every $t$ , so we're done.

24.55 The outcome of all this is that, via the exponential map, local coordinates on

$\mathfrak{g}$ near the zero matrix give us local coordinates on

$G$ near the identity. We call this an exponential coordinate chart.

Optional: Local exponential charts

Local coordinates for GL(n,R)

Local coordinates for matrix groups