The exponential map exp from little g l n R to big G L n R is not invertible, but we have seen that there are neighbourhoods U inside little g l n R of the zero-matrix and V inside big G L n R of the identity matrix such that exp of U equals V and exp restricted to U from U to V is invertible, with inverse log from V to U.
We can think of this as providing for us coordinates near the identity in big G L n R, namely exp of the matrix x_(1,1), dot dot dot, x_(1,n), dot dot dot down to x_(n,n) gives a parametrisation of V, so we can think of the matrix entries x i j as coordinates on V: anything in V can be written in this form for a unique collection of numbers x i j.
We could like the same to work for any matrix group big G inside big G L n R. Namely, we would like to show:
If big G is a matrix group and little g is its Lie algebra then there are neighbourhoods U prime inside little g of the zero matrix and V prime inside big G of the identity such that exp of U prime equals V prime and exp restricted to U prime from U prime to V prime is invertible.
Let U prime be the intersection of U with little g and V prime be the intersection of V and big G. First, we note that exp does indeed go from little g to big G by definition of little g, and exp of U equals V, so exp of U prime is contained in V prime.
So what is left to prove? The map exp from U to V is invertible, hence injective, so its restriction exp restricted to U prime must also be injective. But is exp of U prime surjective? In other words, is it clear that log of V prime is contained in U prime?
This figure shows what you might imagine going wrong (we will later show that this doesn't happen, at least if you shrink U and V). It shows a cartoon of a subgroup big G inside big G L n R which "wraps back on itself" and gets very close to the identity but never quite gets there. You can now imagine that when you intersect with a very small V (in red), exp of U prime (in blue) could end up missing this appendage of big G which wraps back towards the identity (in green), because to get to this appendage you have to exponentiate something very large. In other words, exp of U prime is the blue bit and V prime is everything which is blue or green. In the end, we will show this doesn't happen, so this is a cartoon picture of something which doesn't happen. You therefore shouldn't be too annoyed if the picture doesn't make sense.
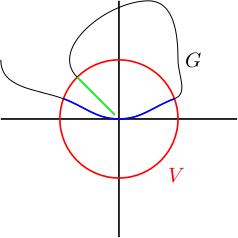
If surjectivity of exp restricted to U prime fails then there's an element g in V prime equals V intersect big G such that g is not in exp of U prime. We could try to fix this by shrinking U and V, but let's suppose that doesn't help us. This will mean there is a sequence g_i in V prime such that g_i tends to the identity and g_i is not in exp of U prime for all i (you should imagine a sequence of matrices on the green appendage, tending to the origin in the picture).
Let's assume that there is such a sequence and aim to derive a contradiction.
Recall that little g inside little g l n R is a subspace. Pick a vector space complement W for little g, that is little g intersects W only at the origin and little g plus W equals little g l n R. In the figure, little g is supposed to be the horizontal axis (tangent to big G at the identity) and W is supposed to be the vertical axis.
I claim that the map F from little g direct sum W to big G L n R defined by F of v, w equals exp of v times exp of w is locally invertible like exp, i.e. there exists a neighbourhood N_1 of the origin in little g direct sum W and a neighbourhood N_2 of the identity in big G L n R such that F of N_1 equals N_2 and F from N_1 to N_2 is invertible. This is proved using the inverse function theorem, just like for exp (compute the derivative of F at the zero map and show this derivative is invertible). I leave it as an exercise to fill in the details.
Therefore, if g_i is sufficiently close to the identity (which it is for large i), then g_i equals exp of v_i times exp of w_i for some sequence v_i in little g and w_i in W.
Our sequence g_i is not in exp of U prime, so w_i is not equal to 0 for all i. In particular, we can divide w_i by its matrix norm to get a matrix w_i over norm w_i with norm 1. Since the set of matrices with norm 1 is closed and bounded (compact), the sequence w_i over norm w_i in W converges to some matrix little w in W with norm 1 (in particular, little w is not zero).
We are going to prove that little w is in little g; this will give us a contradiction, as little w is in W and W is a complement for little g. For this, we need to show that exp of (t times little w) is in big G for all t in R.
Fix t. Consider t over norm w_i and take its integer and fractional parts t over norm w_i equals n_i plus epsilon_i, n_i is an integer, epsilon is in the interval from 0 to 1 including 0 but not 1. Since g_i tends to the identity as i tends to infinity, we know that w_i tends to zero, so norm w_i tends to zero, hence t over norm w_i tends to infinity (as t is fixed) and hence n_i tends to infinity.
We want to show that exp of (t times little w) is in big G. First note that exp of w_i is in G for all i because exp of w_i equals (exp of minus v_i) times g_i and exp of minus v_i and g_i are both in big G. Because big G is a group, (exp of w_i) to the n_i is in big G and (exp of w_i) to the n_i equals exp of (n_i times w_i) because w_i commutes with itself. The sequence exp of (n_i w_i) equals exp of (t w_i over norm w_i, minus epsilon_i w_i) converges to exp of (t times little w) because w_i over norm w_i tends to little w and espilon_i times w_i tends to 0.
Because big G is topologically closed, this limit lives in big G, so exp of (t times little w) is in big G. This argument works for every t, so we're done.
The outcome of all this is that, via the exponential map, local coordinates on little g near the zero matrix give us local coordinates on big G near the identity. We call this an