The determinant gives us a homomorphism det from big G L n R to big G L 1 R, by sending a matrix M to the 1-by-1 matrix with entry det M. This is a homomorphism because det M_1 M_2 equals det M_1 det M_2 and det of the identity equals 1.
Smooth homomorphisms
Homomorphisms
Recap
Recall that a homomorphism is a map F from G to H between two groups such that F of g_1 g_2 equals F of g_1 times F of g_2 for all g_1,g_2 in G and F of 1 equals 1. In other words, F is a map which intertwines the group structures on G and on H. Homomorphisms play a key role in group theory, and we will focus on the case when G and H are matrix groups.
Smoothness
In this course we are trying to use tools from calculus to study groups and homomorphisms, so we would like to be able to differentiate F. You know how to differentiate a function. You know how to differentiate a map from R n to R m by taking partial derivatives of components. But how can we differentiate a map between two matrix groups?
A homomorphism F from G to H of matrix group is
We have exponential maps exp from little g to big G and exp from little h to big H which (as was proved in this optional video) are locally invertible. When we view a map big F from big G to big H in local exponential charts, it means that we get a (locally-defined) map little f from little g to little h which makes this diagram commute:
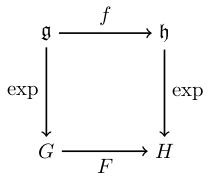
In other words, little f equals log compose big F compose exp wherever that makes sense, i.e. on some neighbourhood of the zero-matrix in little g. This is a map between open subsets of vector spaces little g and little h so it is infinitely-differentiable if all possible iterated partial derivatives of all components exist.
Note that big F of exp X equals exp of little f X for all X in the neighbourhood where little f is defined. You can see this by taking \exp on both sides of little f = log compose big F compose exp.
Main result
If big F from big G to big H is a smooth homomorphism of matrix groups then:
-
little f is the restriction of a linear map big F star from little g to little h to a neighbourhood of the zero-matrix.
-
big F of exp X equals exp of F star X for all X in little g.
-
F star of X bracket Y equals F star X bracket F star Y for all X and Y in little g.
We'll prove this theorem in a later video, but let us remark that this third result is not unexpected: we obtain F star by "taking big F inside the exponential", and the Baker-Campbell-Hausdorff formula told us that the group product exp X times exp Y is determined by X, Y and iterated brackets between them, so if big F preserves group multiplication, it's not surprising that F star preserves the bracket.
Example
Since \det is a homomorphism, this theorem tells us that there is a linear map det star from little g l n R to little g l 1 R such that det of exp X equals e to the det star X for all matrices X. It turns out that det star of X equals the trace of X, that is X_{1,1} + X_{2,2} + dot dot dot + X_{n,n}. So det of exp X equals e to the trace of X
Why is it true that det star of trace? By the theorem, det star is linear, so it suffices to check det star equals trace on a basis for little g l n R.
Let's use the basis of n squared matrices whose entries are all zero except for one which is 1: like 1,0,0,dot dot dot; or 0,1,0,dot dot dot First suppose that we pick a basis element with a 1 on the diagonal, like X equals 1, 0, 0, dot dot dot. Then det of exp X equals det of the matrix with 1s on the diagonal except in one entry you have 1 +1 + a half plus 1 over 3 factorial etc and zeros else where; this sum is e, so we get determinant e, which is e to the 1, and 1 is the trace of X as required.
Pre-class exercise
If X has a 1 on the off-diagonal, I'll leave it as an exercise to check that det of exp of X equals e to the trace of X.