SU(3) overview

SU(3)

0.00 We now turn to the group SU(3), the group of 3-by-3 special unitary matrices. This is an instructive example: its representation theory shares many similarities to the representation theory of other semisimple groups.

0.30 When we studied SU(2), the key tool we introduced was the weight decomposition. In other words, given a representation of SU(2) on a complex vector space V, we decomposed V as a direct sum of subspaces W_k where W_k was a simultaneous eigenspace (with eigenvalue e to the i k theta) for the action of the diagonal subgroup T of diagonal matrices with diagonal entries e to the i theta, e to the minus i theta. This was possible because T is isomorphic to U(1).

0.55 For SU(3), the subgroup of diagonal matrices is isomorphic to U 1 times U 1: T is the set of diagonal matrices with diagonal entries e to the i theta_1, e to the i theta_2, e to the minus i (theta_1 plus theta_2) T here stands for torus: a 2-dimensional torus has two circular coordinates (latitude and longitude) just like U 1 times U 1. For compact matrix groups more generally, the analogue of T will be a (possibly higher-dimensional) maximal torus (more on that later).

4.05 We will postpone the proof until we have seen some examples of weight diagrams. The weight diagrams will now be patterns of dots in the plane.

Examples

The standard representation

Example:

4.30 Take V equals C 3, the standard representation of SU(3) (i.e. considering a matrix in SU(3) tautologically as an element of G L 3 C). We pick the standard basis e_1, e_2 and e_3 in V. We have R of D (theta_1, theta_2) equals the diagonal matrix with diagonal entries e to the i theta_1, e to the i theta_2, e to the minus i (theta_1 plus theta_2)

5.15 so R of D (theta_1, theta_2) e_1 equals e to the i theta_1 e_1, R of D (theta_1, theta_2) e_2 equals e to the i theta_2 e_2, and R of D (theta_1, theta_2) e_3 equals e to the minus i (theta_1 plus theta_2) e_3 so

• e_1 spans the weight space W_{1,0} (k = 1, l = 0).

• e_2 spans the weight space W_{0,1} (k = 0, l = 1).

• e_3 spans the weight space W_(minus 1, minus 1) (k equals minus 1, l equals minus 1).

6.25 The obvious way to represent these would be to simply draw the points (k,l) equals (1, 0); (0, 1); and (minus 1, minus 1) in the plane. For reasons that will become clear when we discuss the Killing form, we will draw the l-axis at 120 degrees to the k-axis. For now, the justification is just that this restores the symmetry we broke when we chose to express the bottom-left entry of D (theta_1, theta_2) in terms of the other two diagonal entries (instead of writing something equally valid like the diagonal matrix with diagonal entries e to the i theta_1, e to the minus i (theta_1 plus theta_3), e to the i theta_3).

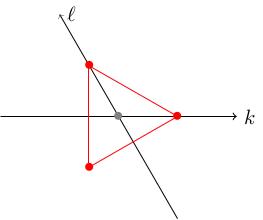
We have also drawn the origin in grey in this picture: it is not a weight of the standard representation, the weights are red.

Sym²(C³)

Example:

8.40 Consider Sym 2 C 3. A basis for this is given by e_1 squared, e_1 e_2, e_1 e_3, e_2 squared, e_2 e_3 and e_3 squared. How do these transform under Sym 2 of D (theta_1, theta_2)?

9.30 Since e_1 maps to e to the i theta_1 times e_1, we have e_1 squared maps to e to the i 2 theta_1 times e_1 squared so lives in the weight space W_{2,0}. Similarly, we get e_1 squared in W_(1,0), e_1 e_2 is in W_(1,1), e_1 e_3 is in W_(0, minus 1), e_2 squared is in W_(0, 2), e_2 e_3 is in W_{minus 1, 0} and e_3 squared is in W_(minus 2, minus 2) For example, e_2 e_3 maps to e to the i theta_2 times e to the minus i (theta_1 plus theta_2) times e_2 e_3, which equals e to the minus i theta_1 e_2 e_3.

11.10 Plotting these weights in the plane (with respect to our tilted axes) we get:

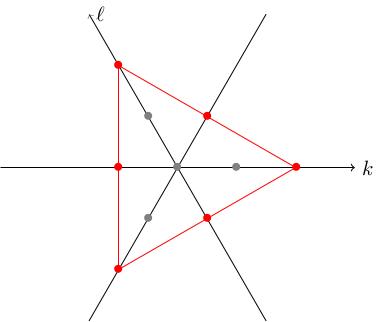
We have also added:

• the line k equals l, to complete the symmetry of the diagram;

• the points (0,0), (1,0), (0,1), (minus 1, minus 1) in grey just to give a sense of the size of the diagram. Only the red dots are weights of the representation.

13.00 The kinds of diagrams we will get for weight diagrams of SU(3) representations will be triangles and hexagons.

Proof of lemma

13.25 Consider the subgroup T_1 consisting of matrices D (theta_1, 0) This is isomorphic to U(1) and V decomposes into weight spaces for the action of T_1: V equals the direct sum of spaces U_k, where U_k is the set of v in V such that R of D (theta_1, 0) applied to v equals e to the i k theta_1 v.

14.40 Define T_2 to be the subgroup of matrices D (0, theta_2).

15.15 This lemma will imply the result because now each U_k decomposes under the action of T_2: U_k equals the direct sum of subspaces W_{k,l} where W_{k,l} equals the subspace of v in U_k such that R of D(0, theta_2) applied to v equals to the i l theta_2 times v. In other words, elements of W_(k,l) transform as desired under both T_1 and T_2 and hence under T: R of D (theta_1, theta_2) applied to v equals R of D (theta_1, 0) times R of D (0, theta_2) applied to v, which equals e to the i (k theta_1 plus l theta_2) times v.

20.05 This argument works more generally for finding weight decompositions of representations of (U 1) to the n: you inductively find the weight space decomposition with respect to (U 1) to the (n minus 1) and show that the final factor preserves the weight spaces (because the group is abelian), then decompose these weight spaces further with respect to the action of the final U(1) factor. This would give us n integer weights k_1 up to k_n and our weight diagrams would be collections of dots in n-dimensional space. For SU(4) we get weight diagrams in R 3, for SU(5) we get weight diagrams in R 4, etc.

Pre-class exercises